Avertissement.

Ce cours est à destination de professionnels qui veulent être informés de cette amélioration technique.

Il a surtout but de vulgariser les principes de réalisation et de conception.

C’est à dire que souvent, je parle d’une « Madame k », constante de son état, qui, du fait de l’utilisation du magnétisme, se trouve omniprésente.

Les calculs complets devraient se servir des notions de Réluctance, qui correspond à la loi d’ohms, en gros pour le magnétisme.

Comme le but de cet ouvrage n’était pas de réinventer ce qui existe déjà, les notions de mathématiques et de physiques sont je l’espère épurées au maximum.

Les puristes seront mécontents, certes ! Ceux qui veulent connaître (et vite), car un chantier les attend, le seront satisfaits, j’espère. C’est uniquement ce qui m’a préoccupé, dans la rédaction de ce cours.

D’autant plus, qu’après la lecture de tout cela, qui dit que certains ne seront pas tentés de reprendre des études ?

Attention, ils se rappelleront, peut-être, de la différence entre la réalité de laboratoire et celle constatée.

Peut-être reconnaitront-ils la présence de « Madame k »

Qu’ils la saluent de ma part, c’est une femme charmante !

Quelques adresses de travail

(La mienne, Mistershoeélec)

http://www.infolytica.com/fr/coolstuff/ex0072/

http://fr.wikipedia.org/wiki/Machine_%C3%A9lectrique#Les_moteurs_sans_balais

http://www.ac-nancy-metz.fr/Pres-etab/loritz/formations/ssi/cours/electrotechnique/moteurPP/moteurPP.htm

http://www.stielec.ac-aix-marseille.fr/cours/abati/axem.htm

http://silicium628.chez-alice.fr/variateur_pour_moteur_brushless/variateur_pour_moteur_brushless.html

http://stielec.ac-aix-marseille.fr/cours/abati/synch.htm#Brush

http://pagesperso-orange.fr/f5zv/RADIO/RM/RM23/RM23B/RM23B12.html

http://fr.wikipedia.org/wiki/Aimantation

Pour les autres adresses, je remercie le travail fait et les présentations récupérés, ou qui m’ont inspirées. Grand merci aussi, pour tous les renseignements fournis.

Par contre, je vous conseillerais de faire toujours attention, aux petites erreurs, surtout dans la présentation de formules et les animations. Sur certain sites, des termes ont étés oubliés, des calculs sont plus ou moins faux, soit les animations bougent, avec des parties (copiés-collés), qui ne sont pas à leur place.

Prudence donc !

Moteurs « à entrefer plan, axial, pas à pas, Brushless, », et autres curiosités.

Préambule :

Ces types de moteurs possèdent au moins, cinq points communs :

· Ils ont un diamètre plus important et une longueur moindre par rapport aux autres types de moteurs.

· L’induction magnétique est gérée axialement pour les moteurs à « entrefer plan » et « axiaux », de manière radiale pour les « Brushless » et « pas à pas ».

· Ils doivent absolument être alimentés en courant continu, même s’il est parfois nécessaire d’intercaler un module électronique de puissance, pour l’alimentation et le pilotage.

· La vitesse doit pouvoir varier dans une grande plage.

· Il est souvent possible de les piloter informatiquement.

Ces moteurs furent conçus pour répondre à une première problématique de volume, jugé souvent important pour les machines à courant continu.

L’usure des structures « collecteur et charbon » et l’entretien délicat et permanent, ont amené les industriels et chercheurs à penser différemment la gestion et la création, des forces mises en évidence par Laplace

Ce furent, par la suite des soucis d’accélération qui prévalurent. Certaines situations industrielles nécessitaient de très grandes accélérations, suivies de très grandes décélérations. Les moteurs continus classiques étaient handicapés par leur masse, leurs volumes et par leur rotor bobiné. A des grandes vitesses, les sections sortaient de leurs encoches et pouvaient bloquer net, le rotor.

Pour terminer, ce fut l’asservissement de position qui justifia cette catégorie de moteur. Par exemple, pour des chaînes de montages automatisées, il était nécessaire de faire tourner un rotor, pour qu’il arrive à un angle donné (programmable, si nécessaire), le plus rapidement possible. Une fois l’angle désiré obtenu, le rotor sera bloqué dans sa position, sans frein extérieur supplémentaire. Il sera possible de choisir un angle différent, inférieur ou supérieur, ce qui amènera le moteur à inverser son sens de rotation ou bien , de devoir travailler à partir d’un point de repos, soumis à forces

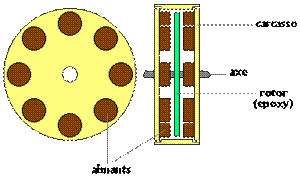
1. Les moteurs à entrefer plan. (Axem)

Ces moteurs furent conçus pour répondre à une première problématique de volume, jugé souvent important pour les machines à courant continu.

Ce furent, par la suite des soucis d’accélération qui prévalurent. Certaines situations industrielles nécessitaient de très grandes accélérations, suivies de très grandes décélérations. Les moteurs continus classiques étaient handicapés par leur masse, leurs volumes et par leur rotor bobiné. A des grandes vitesses, les sections sortaient de leurs encoches et pouvaient bloquer net, le rotor

L’usure des structures « collecteur et charbon » et l’entretien délicat et permanent, ont amené les industriels et chercheurs à penser différemment la gestion et la création, des forces mises en évidence par Laplace.

Principe :

Les lois de Laplace concernant la création de forces électromagnétiques ont été pensées différemment.

L’induction « B » est disposée axialement. Il y aura création d’un couple de forces électromagnétiques, permettant la rotation d’un disque, si ce dernier possède des conducteurs placé perpendiculairement à l’axe et traversé par une intensité.

Comme le conducteur doit se déplacer du fait de la rotation, un autre va le remplacer.

L’alimentation de ces conducteurs ne se fait pas par une structure « collecteur et charbon », mais par une structure de bagues lisses et/ou u peignes d’alimentation. Une alimentation avec une cuve de mercure (conductrice) a été utilisée par l’ancêtre de ce type de moteurs. Ce n’est plus le cas aujourd’hui.

Le magnétisme est réalisé avec des paires d’aimants permanents, ce qui annule les pertes joules provoquées par l’excitation des électroaimants et qui sont constatées, dans les moteurs « classiques ».

l est possible de doubler le couple, en positionnant un balai ou charbon pour obtenir une force supplémentaire qui sera le pendant à la force crée par le brin actif représenté. C’est ce qui est fait le plus souvent ! Cela supprime tout balourd dans la création de l'effort et au point de vue électrique, il y a deux spires en parallèle !

Les balais, ou charbon, ou encore peigne, doivent frotter à la fois sur une lame de cuivre circulaire et sur des lames verticales. Pour éviter une forte usure (comme celle constatée sur des moteurs à collecteur et charbons radiaux), les creux sont comblés avec une résine. Une structure de rattrapage de jeu est cependant nécessaire.

Il n’y a pas à proprement parler de bobinage filaire, seule une plaque de circuit imprimé officie comme telle.

La résistance d'induit est pratiquement nulle. Seuls les phénomènes électromagnétiques seront pris en compte. Le rendement sera excellent et il sera pratiquement exact de dire que :

· P absorbée @ P électrique fournie au disque.

· U x I @ E x I

· U @ E

La machine est réversible, c’est à dire qu’il est possible de s’en servir comme génératrice.

Formules de physique mises en jeu.

Pour connaître E’ moyen = - (E’ en volt) = force contre électromotrice.

Il conviendra de :

· N'utiliser cette règle que pour un seul conducteur gravé sur le disque rotor. (Il est impossible d'insérer ou de graver une bobine)

· S'il y a un deuxième conducteur utilisé, celui-ci est en parallèle. La formule s'appliquera telle quelle.

· Il conviendra de connaître l'induction disponible fournie par les aimants. (c'est le plus difficile) Comme il y a deux aimants identiques, si l'une est connue l'autre le sera aussi. L'induction totale sera le double de celle produite par un aimant.

· F = Produit scalaire de B par la Surface parcourue. B est constant, par contre, S sera fonction du temps. La variation de S se calculera ainsi :

Pour connaître le couple C en Newton mètre.

La formule de Laplace sera nécessaire :

C = Rayon du rotor x B x I x L x sin (angle entre I et B) s’il n’y a qu’une lame alimentée

C = 2 x Rayon du rotor x B x I x L x sin (angle entre I et B) si les 2 lames sont alimentée(en parallèle)

Comme le disque est entraîné en rotation, l’induction ne peut pas être maximale et constante. Par contre, l’angle entre I et B reste à 90°

C = Rayon du rotor x B moyen x I x L x sin(90°) ; comme sin(90°) =1

C = Rayon du rotor x B moyen x I x L, pour une lame seule.

C = Rayon du rotor x B moyen x I x L x 2, pour 2 lames couplées.

Il sera possible d’estimer la variation relative de B en fonction de l’éloignement des lames, en constatant que celle-ci est produite par la décomposition de B en 2 composantes vectorielles.

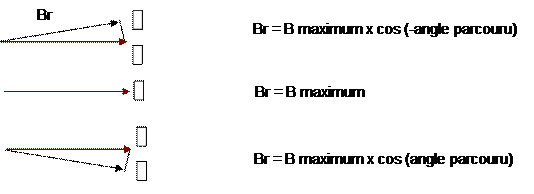
Ce qui amènera la variation de Br suivante, en fonction de l’angle parcouru.

L’écart d’angle de calculera en effectuant le rapport : 360° / nombre de lames.

L’écart d’angle = 2 x a

a = 360° / nombre de lames / 2

B moyen sera approximativement égal à

B moyen = (B maximum + B maximum x cos (a))/2

(Compte tenu de la petitesse de l’angle la différence avec la rigueur d’un calcul intégral de moyenne sera des plus minimes)

Le couple deviendra

C = Rayon du rotor x (B maximum + B maximum x cos (a)) / 2 x I x L

Ou

C = Rayon du rotor x (B maximum + B maximum x cos (a)) / 1 x I x L (s’il n’y a qu’une lame alimentée)

La puissance sur le rotor.

P utile = 2 x p x n x C

Pu =2 x p x n x Rayon du rotor x B moyen x I x L, pour une lame seule.

Ou

Pu =2 x p x n x Rayon du rotor x B moyen x I x L x 2, pour 2 lames couplées

Si l’on admet que U @ E et que Pabsorbée @ Pélectrique transmise @ Putile ; l’expression de la force contre électromotrice E’, deviendra, par comparaison :

E x I @ Pu =2 x p x n x Rayon du rotor x B moyen x I x L @ U x I

(Pour les rotors à une seule lame couplée)

Ou

E x I @ Pu =2 x p x n x Rayon du rotor x B moyen x I x L x 2 @ U x I

(Pour les rotors à 2 lames couplées)

Ce qui au final amène par simplification avec I

E @ U @ 2 x p x n x Rayon du rotor x B moyen x L

(Pour les rotors à une seule lame couplée)

E@ U @ 2 x p x n x Rayon du rotor x B moyen x L x 2

(Pour les rotors à 2 lames couplées)

Pour la vitesse, il suffira de faire le rapport.

n @ U/(2 x p x Rayon du rotor x B moyen x L)

n @ E/(2 x p x Rayon du rotor x B moyen x L)

(Pour les rotors à une seule lame couplée)

Ou

n @ U/(2 x p x Rayon du rotor x B moyen x Lx2)

n @ E/(2 x p x Rayon du rotor x B moyen x Lx2)

(Pour les rotors à une seule lame couplée)

Il est à remarquer que la vitesse va varier inversement et proportionnellement avec l’induction. (Comme pour les machines à courant continu classiques)

Avantages et inconvénients de ce type de structures.

Le moteur est à courant continu. Il est possible de faire varier la vitesse, grâce à un variateur de tension du type « Rectivar ».

Le couple fourni sera directement fonction de l’induction de la tension d’alimentation.

Le moteur ne peut pas caler, brutalement, comme les moteurs asynchrones. Par contre le moteur peut ralentir en fonction du couple résistant imposé.

Certains constructeurs intègrent une dynamo tachymétrique sur l’arbre moteur, en vue de faire d’asservir la vitesse du moteur.

Il n’est pas possible d’agir sur l’induction car, il n’y a pas de bobinage d'excitation. De ce fait, il n’y a aucun risque de voir ce type de moteur s’emballer suite à une rupture de production de flux.

Il n’y a pas de pertes joules inducteur.

Il n’y a pas de masse ferreuse importante au rotor, certains sont même réalisés en matières plastique. Ceci entraînera une constante de temps électrique faible (L/R) Le moment d'inertie sera très faible ; la constante de temps mécanique est très faible. Les accélérations et décélérations pourront être très fortes.

Le moteur sera plus large que long. Il sera en volume brut, de taille moins importante et beaucoup plus léger que ses confrères utilisant le principe d’excitation radiale.

Du fait de la disposition des conducteur et des peignes, il y aura très faible réaction d'induit.

L’inversion pourra se faire par inversion directe de la tension d’alimentation. Il n’est pas possible d’utiliser ce type de moteur en mode « universel ». L’alimentation en courant alternatif est donc proscrite.

Les intensités dans l’induit seront très fortes. Les densités de courant dans le bobinage (circuit imprimé) aussi.

Comme les espaces sont limités, les écoulements thermiques ne seront pas facilités, ce qui ne permet pas au moteur de tolérer des surcharges trop longues.

Remarque importante (dixit les constructeurs)

« Le démontage du moteur a pour conséquence une désaimantation. Cette opération est donc à proscrire, lorsqu'on ne dispose pas du matériel nécessaire à une ré aimantation du moteur après remontage. »

Télécharger une notice :

http://www.stielec.ac-aix-marseille.fr/cours/abati/datasheet/axem.pdf

2. Les moteurs de flux axiaux.

Ces moteurs furent conçus pour répondre à une première problématique de volume, jugé souvent important pour les machines à courant continu.

Ce furent, par la suite des soucis d’accélération qui prévalurent. Certaines situations industrielles nécessitaient de très grandes accélérations, suivies de très grandes décélérations.

Il existe deux types de modèles, fondamentalement identiques : une source de magnétisme fixe est mise en confrontation avec une source de magnétisme tournante.

Soit le rotor est constitué d’électroaimant, constitués de bobines avec noyau.

Soit, il n’y a que des bobines, sans noyau. Ces dernières présentent une inertie moindre qui permet des accélérations extrêmes.

Les bobines peuvent comporter plusieurs spires, mais comme les force-contre électromotrice sont importantes, elle sont le plus souvent constituée de barreaux conducteurs uniques. Ce qui augmente la solidité de l’ouvrage aux forces centrifuges.

Il y a un nombre pair d’aimants permanents. Le plus souvent le nombre est deux ! (Ce n’est pas une obligation.

Une commutation de l’alimentation des bobines est nécessaire. Elle s’effectuera de manière automatique par un jeu de lames d’alimentation, disposées de manière à créer un flux magnétique qui permettra l’attraction du rotor par un des aimants permanents du stator. Quand celle-ci sera optimale, l’alimentation cessera, par contre une deuxième bobine prend le relais et ainsi de suite.

Ce type de moteur ne permet pas l’asservissement de position. Il tourne en permanence.

La vitesse dépendra de la tension d’alimentation des bobines. Plus le nombre de bobine est important, plus le moteur est souple et moins il y a de saut, dans la création du couple moteur.

(Photographie récupérée pour le cours sur Infolytica) http://www.infolytica.com/fr/coolstuff/ex0072/

A. Construction du bobinage :

Le plus souvent le nombre d’aimants permanents opposés est 2. Il peut être supérieur, mais il sera toujours pair !

Chaque bobine sera le plus souvent constituée de 2 demi-barreaux soudés. Chaque demi-barreau forme un faisceau.

Le pas fait partie de la famille des « diamétraux ». C'est-à-dire que si un faisceau est face au début d’un pôle, le deuxième faisceau constituant la section se trouve au début immédiat du deuxième pôle, ou décalé de 1, ou 2 (pas plus). Chaque bobine est identique aux autres.

Exemple :

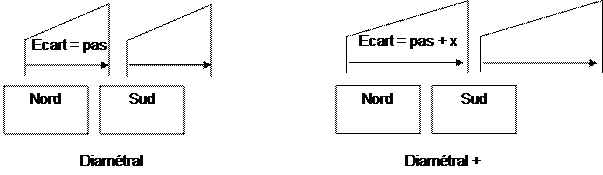
Le bobinage sera constitué d’un nombre  « G », de groupe de bobines.

Plus « G » sera important, plus le moteur sera souple, et subira peu d’à-coup.

L’angle parcouru par le rotor sera égale à 360°/nombre total de bobines (ou de raccords) entre les bobines.

Par réalité pratique, il y aura deux faisceaux, par bobine.

Par groupe il y aura un nombre « n » de bobines, égale au nombre de pôles. Chacune des bobines sera en série avec la précédente du même groupe.

Les bobines seront disposées à plan et strictement, en avant.

L’ensemble constituera, comme pour les moteurs à courant continu classique, un ensemble de 2 demi-groupes en parallèle, de n/2 bobines en série, d’un groupe.

Les connections serviront à la fois de raccord entre faisceau et point d’alimentation.

Les bobinages se calculeront comme ceux des machines à courant continu classiques :

· Soit le pas est strictement diamétral. Dans ce cas le nombre de bobines utiles sera égale au nombre de bobines par groupe. Chaque bobine est en parallèle. Cette solution est utilisée si l’on veut beaucoup de couple. Le nombre de pôles est le plus souvent 2.

· Soit le pas est diamétral + (quelque chose) Dans cette optique les bobinages vont se chevaucher et la conception sera strictement identique à celle des machines à courant continu de type radial. Les bobines d’un groupe seront séparées en deux sous-groupes. Les bobines d’un « sous-groupe seront en série et chaque sous groupe sera en parallèle avec l’autre. Cette solution est utilisée si l’on veut beaucoup de variation de vitesse. Le nombre de pôles est le plus souvent 2.

· Il est possible de combiner couple et vitesse en ayant 4, pôles ou plus. Si cette solution est envisagée, il faudra réaliser des connexions. supplémentaire en augmentant le nombre de galets. Celui ci devra être égal au nombre de pôles. Cette solution est peu ou pas utilisée, car un des objectifs de la réalisation de ce type de moteur est de diminuer coûte que coûte, les frottements. Cette pratique nous en éloigne.

B. Le pas est strictement diamétral.

Les bobines sont proches, jointives et se trouvent réunies par une soudure.. Une paire de galets conducteurs assurera, ou non l’alimentation.

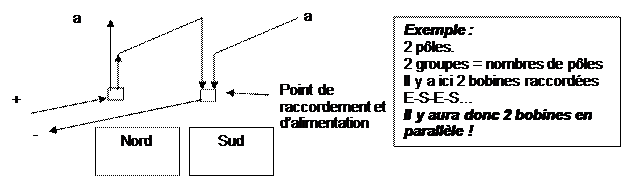
Un exemple :

Un moteur de 8 bobines et 2 pôles.

N = nombres de bobines par groupe = nombres de pôles = 2

Nombre de groupe = nombres de bobines / nombres de bobines par groupe

= 8/2 = 4

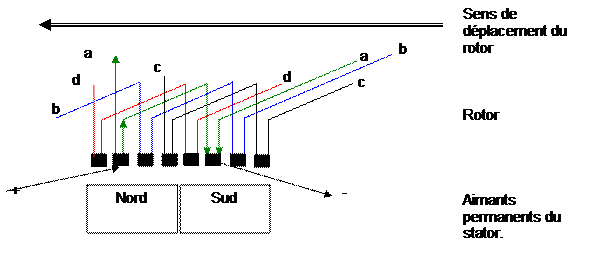
Les galets d’alimentations se placeront, là où se trouvent les flèches.

Séquence :

Le groupe précédent se déconnecte.

Le groupe « a » va créer une paire Sud Nord. Le rotor se déplace vers la gauche.

Le groupe précédent se déconnecte.

Le groupe « b » va créer une paire Sud Nord. Le rotor se déplace vers la gauche.

Le groupe précédent se déconnecte.

Le groupe « c » va créer une paire Sud Nord. Le rotor se déplace vers la gauche.

Le groupe précédent se déconnecte.

Le groupe « d » va créer une paire Sud Nord. Le rotor se déplace vers la gauche.

Etc.

L’angle parcouru entre chaque commutation sera égal à 360°/8 = 45°

Un autre exemple :

Un moteur de 16 bobines et 4 pôles, avec connections parallèles.

N = nombres de bobines par groupe = nombres de pôles = 4

Nombre de groupe = nombres de bobines / nombres de bobines par groupe

= 16/4 = 4

Il devra y avoir 4 galets d’alimentation 2 pour le « + » et 2 pour le « - »

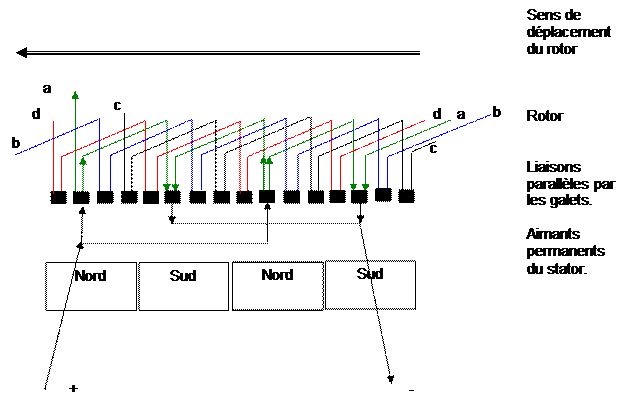
Les galets d’alimentations se placeront, là où se trouvent les flèches.

Une connexion parallèle est nécessaire. Tout se passera comme si 2 moteurs étaient connectés en parallèle. La puissance sera doublée par rapport à l’exemple précèdent.

Séquence :

Elle sera identique dans le principe. Par contre l’angle parcouru sera 2 fois plus faible que dans le premier exemple.

C. Le pas diamétral +

Généralement ce sera + 1 ou +2, pas davantage pour restreindre les contraintes de positionnement de bobinage et de cuivre. Il y aura autant de liaisons parallèles, qu’il y aura de paires de pôles.

D. Principes physiques et formules.

Principe de fond :

Une bobine fixe va brutalement produire un champ magnétique de type « continu », au voisinage d’une source d’aimantation complémentaire, qui elle peut-être mobile.

S’il existe un décalage de position entre les deux sources magnétiques, alors la source mobile va être attirée selon la règle du flux maximal.

Il sera possible qu’il y ait une répulsion, car l’alimentation des bobines fixes dépend exclusivement de la position de broches d’alimentation, donc de la position de la source magnétique, mobile.

Exemple :

Une remarque :

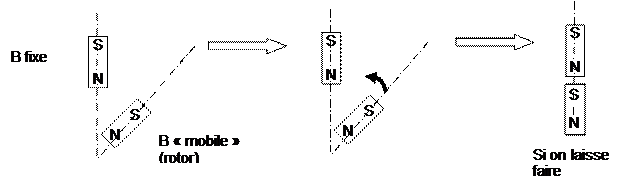
La position extrême, celle où les deux sources magnétiques sont face à face n’est pas utilisée. En effet, celle-ci permet un asservissement en position, par contre, elle nécessiterait une dépense d’énergie supplémentaire, pour décoller et un temps d’arrêt préjudiciable, au principe de choix d’un moteur avec une accélération maximale.

Il est donc constaté la rupture de l’alimentation de la source magnétique fixe la plus proche de la partie mobile et l’alimentation de la 1^ère bobine toute juste voisine de la plus proche.

A constater : Les aimants permanents passent devant les bobines fixes et les chevauchent.

Ce qui amène un fonctionnement du type de celui, ci-dessous.

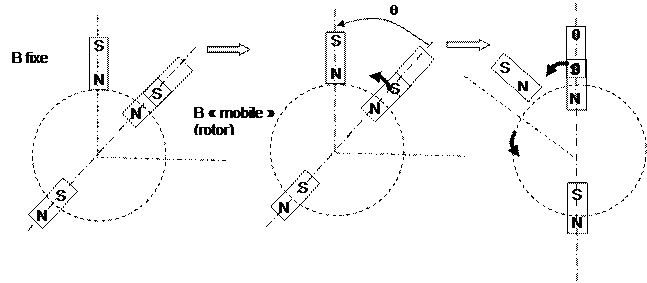
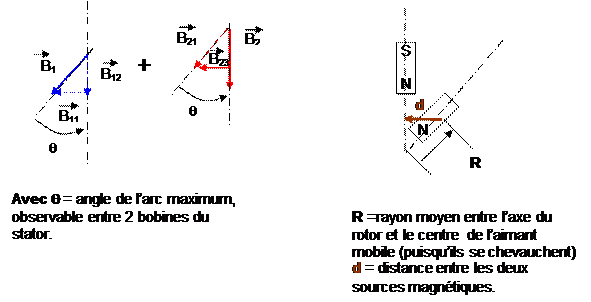
Avec q = angle de l’arc maximum, observable entre 2 bobines du stator.

Ce qui entrainera une nouvelle attraction (et aussi une répulsion). A chaque commutation, au niveau des broches, le phénomène se reproduira. Ce qui entrainera un mouvement particulier, où une source magnétique tentera de rattraper, sans y parvenir totalement, une autre source mobile qui tente de lui échapper.

L’analogie la plus parlante serait celle d’un leurre en tissu, censé symboliser un lapin et qui va courir devant des lévriers.

Au point de vue lois physiques et magnétiques.

Il existe une loi magnétique, relative à la force d’attraction ou de répulsion, produite par deux aimants :

F = (B₁ +B₂)² / (4.P.e₀ . d²)

B₁, B₂ correspondent aux intensités magnétiques des deux aimants.

d² est la distance linéaire entre les deux aimants

e₀ est une constante fixe, égale à 885 .10¹²

Ceci sera presque vrai, car l’estimation est plus complexe, il faudrait tenir comptes des surfaces et de l’écartement entre les surfaces.

La formule serait plutôt :

F = k. (B₁ +B₂)² / (4.P.e₀ . d²)

k serait = 1 si les surfaces se touchent,

k <1 s’il elles sont plus ou moins éloignées.

Une « bonne » approximation sera faite

Avec 0,8 <k <1

Un autre problème sera de retrouver (B₁+B₂), en fonction de la position, donc de d².

Prenons une position.

Les deux sources sont décalées, les vecteurs le sont aussi, mais ils peuvent être l’un et l’autre, décomposés en vecteurs élémentaires comprenant une composante verticale et horizontale.

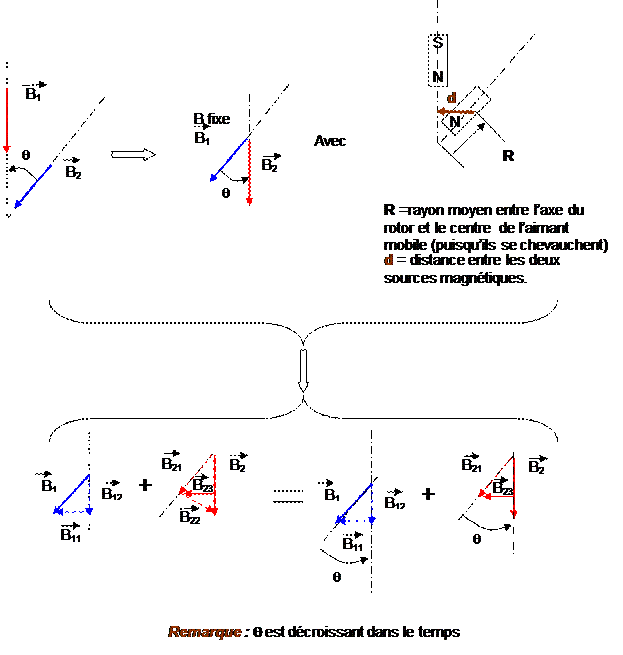
Si l’on analyse les projections des vecteurs, il est possible de constater qu’une partie du vecteur B₂ ne participe pas, ou ne participe plus à la création de la force.

Les vecteurs participants seront : B₁₁ et B₂₃

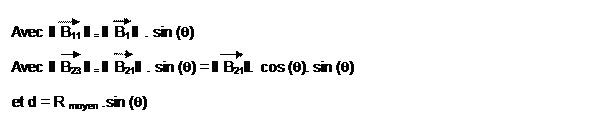
La formule générale de F produite par une bobine

F = k . (B₁ + B₂)² / (4.P.e₀ . d²) où, B₁.B₂, correspondent à B₁₁ et B₂₃

Ce qui amènera à :

F = k . (B₁₁ + B₂₃)² / (.P.e₀ . [r _moyen .sin(q)]²)

F =k . [B₁ . sin (q) + B₂. cos (q) . sin (q) ] ² / (4P.e₀ . [r _moyen .sin (q)]²)

Les «sin» disparaissent par simplification…………….. !

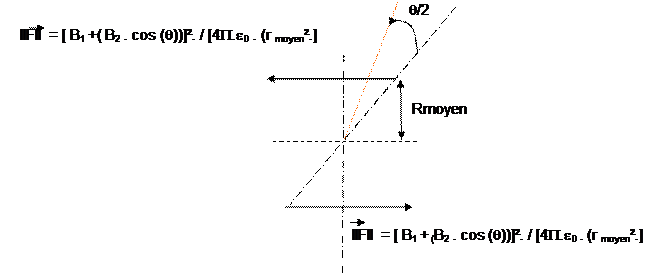
F = k. [ B₁ + B₂ . cos (q)]². / [4P.e₀ . (r _moyen².]

K reste le coefficient réducteur lié à l’écartement et la forme des sources magnétiques.

L’angle parcouru sera général un peu supérieur à la moitié de l’arc existant entre deux bobines du stator. Ceci permettra d’éviter que l’aimant permanent du rotor et la bobine soit en attraction maximale et qu’un ralentissement soit observé !

Cf remarque

Couple produit

· Moteurs bipolaires :

Le couple total sera égal à 2 fois cette expression fois l’écart entre les deux forces,

Le couple C = k . 2 . F r _moyen Celui-ci dépendra de q (et donc du temps)

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

C = k . 2 . [ B₁ + B₂ . cos (q)]².r moyen / [4P.e₀ . (r _moyen².]

= 2. [ B₁ + B₂ . cos (q)]²/ [4P.e₀ . (r _moyen.]

C = (en Nm) = k . 2 . [ B₁ + B₂ . cos (q)]²/ [4P.e₀ . (r _moyen.]

Après simplification.

Le couple C = 2.F. r _moyen = k . [B₁ + B₂ . cos (q)]²/ [ 2 P . e₀ . (r _moyen.]

(en Nm)

Avec 0,8 <k <1

· Moteurs multipolaires.

Le couple sera fonction du nombre de paires de pôles.(p) et dépendra de q (et donc du temps)

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

Le couple C = 2.F. r _moyen .p =k .p.2. [ B₁ + B₂ . cos (q)]²/ [4P.e₀ . r _moyen.]

(en Nm)

Après simplification.

Le couple C = k . 2.F. r _moyen .p = k .p. [ B₁ + B₂ . cos (q)]²/ [ 2P . e₀ . (r _moyen.]

(en Nm)

Avec 0,8 <k <1

· Variation du couple en fonction de q, pour un bobine de stator étudiée.

·

Le couple ne sera pas constant.

Cmoyen @ (C1 + C2 )/ 2

Cmoyen @ C = (en Nm) = k . [ [ B₁ + (B₂ . cos (0))]²/ [2 P.e₀ . (r _moyen.]

+ [ B₁ + (B₂ . cos (q/2))]²/ [2 P.e₀ . (r _moyen.] ] / 2

Avec 0,8 <k <1

(On effectue cette approximation, car q est faible, l’erreur est minime. Par contre les fanatiques matheux peuvent et doivent dégainer Un calcul de moyenne, avec les intégrales)

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

q, correspondra à un angle qui se calculera en divisant 360° par le nombre de bobines du stator.

q = 360/N _bobines
Si l’on prend en compte des autres bobines du stator, celles-ci vont produire avec les pôles de l’aimant permanent du rotor d’autres éléments de couple.

Ceci amènera une ondulation pour le couple en fonction du temps.

Un constat : Plus il y aura de bobines sur le stator plus les ondulations seront rapides et de faibles amplitudes.

Calcul des bobinages

Comment calculer le bobinage ?

a) Il faudra connaître les deux inductions magnétiques mises en jeu ou possibles.

· B₁ dépendra du châssis magnétique choisi et de la bobine. Il faudra connaître le maximum possible sans saturation. Il existe une méthode sur le site « Mistershoeélec » en catégorie « bobinage ».

· B₂ sera fixe et dépendra des aimants permanents.

b) Il faudra aussi connaître la manière dont le bobinage est réalisé. Dans la plupart des cas, les moteurs sont bipolaires et les bobines sont groupées en deux ensembles en parallèle, de bobines, elles, reliées en série.

Exemple : 4 bobines en tout = 2 groupes de 4 bobines. Les 4 bobines sont en série, les 2 groupes sont en parallèle.

Nous aurons pour une bobine

E = N.(B₁ + B₂). Lo . n . 2P. R _moyen

N= E / (B₁ + B₂). Lo . n . 2P. R _moyen

Avec n = vitesse de rotation de la partie mobile, en tours par seconde.

N = nombre de spires

Lo= longueur de bobine

Rb = rayon de la bobine

Quelques notions supplémentaires

Magnétismes mis en présence.

· B2 est produit par un aimant permanent.

· B1 est produit par une bobine « plate »

C'est une bobine beaucoup plus large que longue qui comporte généralement plus d'une spire et dont l'induction en son centre vaut :

Le problème sera de connaître I (intensité)

Si l’on contourne la difficulté en déterminant les variations de flux.

Tension nécessaire

E = N . dj/dt = (B₁+ B₂ ). Lo . dx/dt

Avec dx/dt = vitesse tangentielle de rotation de l’aimant permanent = n . 2P. R moyen

n = vitesse de rotation de la partie mobile, en tours par seconde.

N = nombre de spires

Lo= longueur de bobine

Rb = rayon de la bobine.

Lo . dx = variation de surface.

La formule deviendra :

E = N . dj / dt = (B₁+ B₂ ). Lo. dx/dt = N . dj/dt = N . (B₁+ B₂). Lo . n . 2P. R _moyen.

E = N.(B₁+ B₂). Lo . n . 2P. R _moyen

Ce qui sera suffisant par un technicien souhaitant calculer un nombre de spires

Intensité consommée

La bobine « plate » aura pour coefficient d’auto induction L = N . j / I = m0. N² /2Rb

Et e(V) = L di/dt

E = (B₁ + B₂). Lo . n . 2P. R moyen = L di/dt

Ce qui implique que si E est brutalement appliqué et constant ainsi que B₁, B₂, i sera de forme affine (c’est un calcul intégral)

Tel que i (t) = E . t / L

I va progresser le temps d’alimentation d’une bobine et aura la forme suivant.

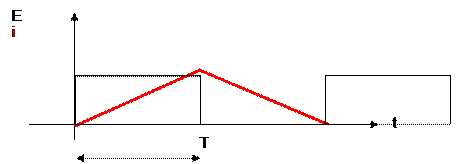
T sera le temps d’alimentation d’une bobine. Ce temps sera fonction de la rotation du rotore et, par la même du temps de commutations des sections par le rotot ce qui, on le rappelle permet alimentation de l’inducteur du moteur.

· I moyen = E.T/L/2

· Si l’on veut I efficace, pour la section des fils = E.T/L/ 1,414

L = coefficient d’auto induction d’une bobine :

L = (m0. N² /2Rb S _{surface de la bobine}) / L _{longueur de la bobine} (si μ₀ et μ_r sont connus)

Sinon, la bobine possédera un coefficient L donné qu’il est possible de mesurer par une méthode « voltampèremétrique », en alternatif, et continu, par la méthode des impédances.

Pour trouver Z = U _continu / I _continu pour avoir R,

Pour trouver Z = U_alternatif / I _alternatif et continu, par la méthode des impédances.

L = Racine carré de (Z² -R²)/2π.f

Ce qui sera suffisant par un technicien souhaitant calculer un nombre de spires et la section.

Couple et Puissance mécanique mis en jeu

Cmoyen (Nm) @ 2. k .F. r _moyen . p = p . [ B₁ + B₂ . cos (q)]²/ [ 2P . e₀ . (r _moyen.]

Avec p = nombres de paires de pôles.

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

Avec 0,8 <k <1

P (Watts) = 2 . P .n .C

Avec n = vitesse de rotation en tours/secondes.

c) Les moteurs sans balais, de type Brushless.

Ces moteurs sont de type « Radial ».

Il existe deux types de modèles, mais au final, le principe est le même : une source de magnétisme fixe est mise en confrontation avec une source de magnétisme tournante.

Soit le rotor est visible de l’extérieur, soit il est disposé de manière classique.

Il est généralement constitué d’aimants permanents, pour les plus modernes et les plus compacts ; ou d’électro-aimants, pour les plus importants.

Pour ces derniers, l’alimentation se fait en courant continu et par un jeu de 2 bagues conductrices. Le moteur est plus robuste, mais il a plus d’inertie. Ce type de moteur fait partie d’un ensemble nommé « Brusless », ou « Moteur sans balais ».

Le rotor peut constituer la cage extérieure (brushless out-runner).

Une adresse des plus intéressantes pour les amateurs de modélismes :

http://www.legallou.com/Modelisme/Brushless/IndexBrushless.html

Travail du bobineur :

Refaire si possible et à l’identique, le bobinage d’une ou de plusieurs bobines sur le stator.

Il est parfaitement déconseillé de ne pas laisser trainer des outils ou de la limaille sur le rotor sous peine de voir l’ensemble de dé-aimanter.

Le stator peut constituer la cage extérieure (brushless out-runner).

Les bobines du stator seront alimentées  (cas de l’image gauche) :

· Soit, en courant continu, haché, qui sera fourni par un module électronique de puissance.

Pour les faibles puissances (<0,1cv), les moteurs prennent surtout le nom de « moteurs pas à pas », chez les professionnels.

Pour les puissances (>0,1cv), les moteurs prennent surtout le nom de « Brushless », chez les professionnels.

Les bobines seront câblées en étoile. Le module d’alimentation disposera d’autant de phase qu’il y aura de bobines. Le moteur pourra être couplé avec un capteur rotatif, ce qui permettra un asservissement de position. Le rotor sera exclusivement constitué d’aimants permanents.

· Soit en courant alternatif sinusoïdal polyphasé. (Cas de l’image de droite). L’ensemble prendra surtout le nom de machines auto synchrones chez les professionnels. Ce sera généralement des moteurs asynchrones à rotor bobiné (6 bobines) qui seront utilisés. Dans ce cas le moteur sera alimenté au démarrage, comme un moteur asynchrone classique avec les bobines des électroaimants du stator monté en étoile, non alimentées et en court-circuit. Lorsque le moteur sera lancé et que la vitesse sera maximale, il conviendra d‘alimenter les bobines en courant continu. Le rotor va accrocher le champ tournant et la vitesse du rotor deviendra égale à la vitesse du synchronisme du moteur. La machine tournera alors de manière dite « synchrone ». Il sera possible de faire varier la vitesse du moteur, en usant d’un variateur de fréquence.

Principes physiques et formules pour un moteur à rotor extérieur (brushless out-runner).

Principe de fond :

Une bobine fixe va brutalement produire un champ magnétique de type « continu », au voisinage d’une source d’aimantation complémentaire, qui elle peut-être mobile.

S’il existe un décalage de position entre les deux sources magnétiques, alors la source mobile va être attirée selon la règle du flux maximal.

Il sera possible qu’il y ait une répulsion, car l’alimentation des bobines fixes dépend exclusivement de la position de broches d’alimentation, donc de la position de la source magnétique, mobile.

Exemple :

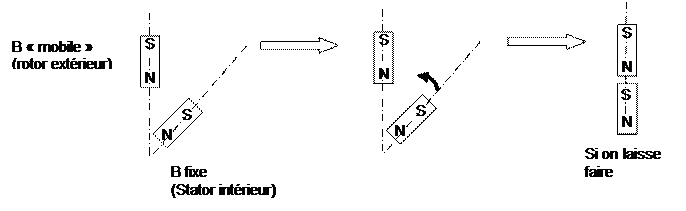
Le moteur pourra avoir deux statuts :

· En rotation. Il fonctionnera comme un moteur classique, la vitesse dépendra de la fréquence de l’horloge de commande du module électronique de l’alimentation.

· Statique, sur une position choisie, si l’on bloque à 0, la fréquence de l’horloge de commande du module électronique de l’alimentation.

Remarque :

La position extrême, où les deux sources magnétiques sont face à face, peut être utilisée. En effet, celle-ci permet un asservissement en position, par contre elle nécessite une dépense d’énergie supplémentaire, pour décoller et un temps d’arrêt. Dans ce cas Le moteur de comporte comme un moteur dit « Pas-à- pas »

Les aimants fixes et les électroaimants vont respectivement présenter un flux magnétique, caractérisé par une présentation axiale. Ce flux est constant quelque soit l’importance de la surface.

Il est par contre nécessaire de connaître les surfaces mise en jeu, dans la génération de ce flux.

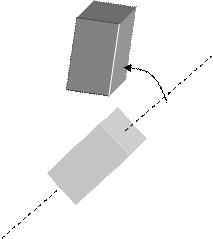
L’alimentation des bobines sera réalisée par un circuit électronique de puissance. Celui-ci alimentera de façon séquentielle chacune des bobines du stator central.

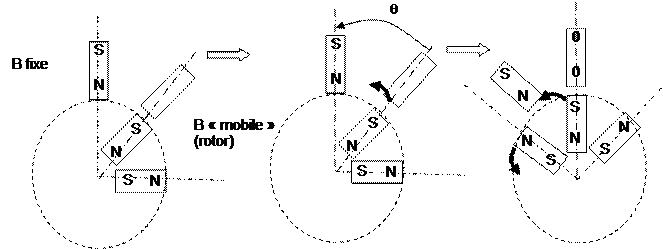
Avec q = angle de l’arc maximum, observable entre 2 bobines du stator.

Ce qui entrainera une nouvelle attraction (et aussi une répulsion). A chaque changement dans l’alimentation des bobines (phases) le phénomène se reproduira. Ce qui entrainera un mouvement particulier, où une source magnétique tentera de rattraper, sans y parvenir totalement, une autre source mobile qui tente de lui échapper.

Au point de vue lois physiques et magnétiques.

Il existe une loi magnétique, relative à la force d’attraction ou de répulsion, produite par deux aimants :

F = (B₁ ⁺ B₂)² / (4.P.e₀ . d²)

B₁, B₂ correspondent aux intensités magnétiques des deux aimants.

d² est la distance linéaire entre les deux aimants

e₀ est une constante fixe, égale à 885 .10¹²

Ceci sera presque vrai, car l’estimation est plus complexe, il faudrait tenir comptes des surfaces et de l’écartement entre les surfaces.

La formule serait plutôt :

F = k. (B₁ +B₂)² / (4.P.e₀ . d²)

k serait = 1 si les surfaces se touchent.

k <1 s’il elles sont plus ou moins éloignées.

Le problème consistera à retrouver B₁+B₂ , en fonction de la position donc d².

Prenons une position.

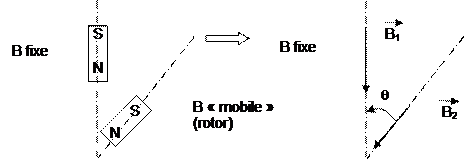
Les deux sources sont décalées, les vecteurs le sont aussi, mais ils peuvent être l’un et l’autre, décomposés en vecteurs élémentaires comprenant une composante verticale et horizontale.

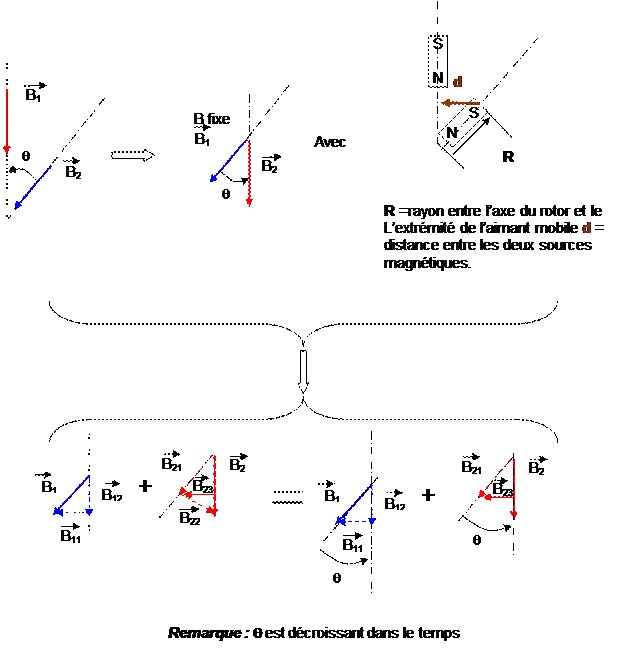
Si l’on analyse les projections des vecteurs, il est possible de constater qu’une partie du vecteur B₂ ne participe pas, ou ne participe plus à la création de la force.

Les vecteurs participants seront : B₁₁ et B₂₃

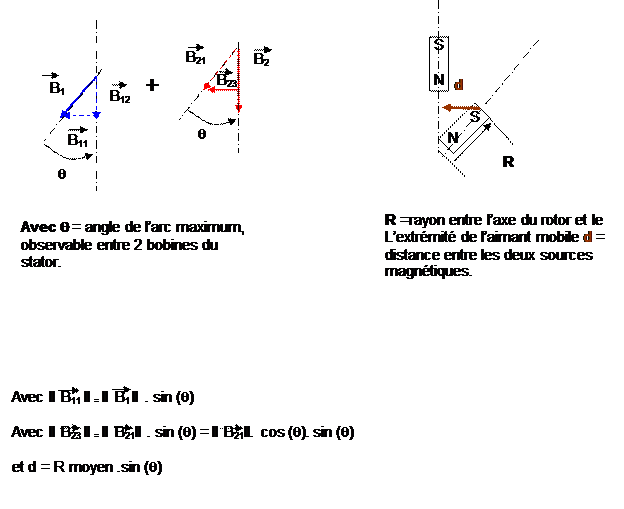
La formule générale de F produite par une bobine

F = (B₁ + B₂)² / (4.P.e₀ . d²) où, B₁ + B₂, correspondent à B₁₁ et B₂₃

Ce qui amènera à :

F = (B₁₁ + B₂₃)² / (.P.e₀ . [r .sin(q)]²)

F = [B₁ . sin (q) + B₂. cos (q) . sin (q) ]² / (4P.e₀ . [r.sin (q)]²)

Les « sin » disparaissent par simplification…………….. !

F = k. [ B₁ + B₂ . cos (q)]². / [4P.e₀ . r ².]

K reste le coefficient réducteur lié à l’écartement et la forme des sources magnétiques.

L’angle parcouru sera général un peu supérieur à la moitié de l’arc existant entre deux bobines du stator. Ceci permettra d’éviter que l’aimant permanent du rotor et la bobine soit en attraction maximale et qu’un ralentissement soit observé !

Cf remarque

Travail du bobineur :

Refaire si possible et à l’identique, le bobinage d’une ou de plusieurs bobines sur le stator.

Il est parfaitement déconseillé de bricoler le rotor sous peine de voir l’ensemble de dé-aimanter.

S’il faut, maintenant, quelques théories, ou « Comment calculer le bobinage ? »

Tension nécessaire pour une bobine inductrice.

a) Il faudra connaître les deux inductions magnétiques mises en jeu ou possibles.

· B₁ dépendra du châssis magnétique choisi. Il faudra connaître le maximum possible sans saturation et de la bobine de phase. Il existe une méthode sur le site « Mistershoeélec » en catégorie « bobinage ».

· B₂ sera fixe et dépendra des aimants permanents.

E = N.(B₁+ B₂). Lo . n . 2P. R

Avec :

E = tension maximum imposée à la bobine inductrice.

dx/dt = vitesse tangentielle de rotation de l’aimant permanent = n . 2P. R

n = vitesse de rotation de la partie mobile, en tours par seconde.

N = nombre de spires

Lo = longueur de bobine, en m.

R = Rayon du rotor ou de la roue polaire, en m

Ce qui sera suffisant par un technicien souhaitant calculer un nombre de spires

Intensité dans une bobine.

· I moyen = E.T/L/2

· Si l’on veut I efficace, pour la section des fils = E.T/L/ 1,414

L = coefficient d’auto induction d’une bobine :

L = ( μ₀ . μ_r . N² . S _{surface de la bobine}) / L _{longueur de la bobine} (si μ₀ et μ_r sont connus)

Sinon, la bobine possédera un coefficient L donnée qu’il est possible de mesurer par une méthode « voltampèremétrique », en alternatif, et continu, par la méthode des impédances.

Pour trouver Z = U _continu / I _continu pour avoir R,

Pour trouver Z = U_alternatif / I _alternatif et continu, par la méthode des impédances.

L = Racine carré de (Z² -R²)/2π.f

Ce qui sera suffisant par un technicien souhaitant calculer un nombre de spires et la section.

Couple et forces produites :

a) Couple produit en rotation.

· Moteur avec une seule bobine seule, alimentée :

Cmoyen @ k . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)

Avec 0,8 <k <1

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

· Moteur avec plusieurs bobines alimentées en même temps bobine (N_bob) :

Cmoyen @ k . N_bob . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)

Avec 0,8 <k <1

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

b) Force de contact.

Elle dépend exclusivement des intensités magnétiques de l’aimant permanent et de l’électroaimant et de la surface d’exposition.

F = (B₁ + B₂)² x Surface en contact) / (2 x m₀) ¹

Avec : m₀ = 4.p10^-7 en H.m^-1

S en m²

F en Newtons

F = (B₁ x B₂ x S) / (2 x m₀)

c) Nombre de saut, ou de pas.

Le nombre de positions obtenues sera égal au produit nombre de bobines inductrices par nombre de pôles des aimants permanents.

d) L’angle parcouru par « pas »

Il sera égal à 360° / nombre de pas

Explications

· Moteurs avec une seule bobine seule, alimentée :

Le couple total sera égal F fois l’écart entre l’application de la force et le rayon du rotor,

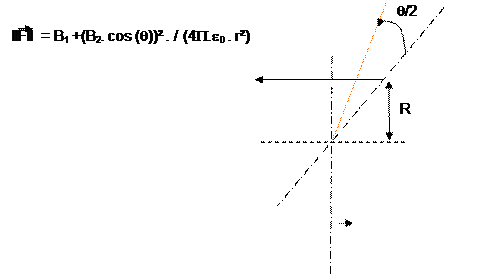
Le couple C = F r

= k . (B₁ + (B₂. cos (q))² .r / (4P.e₀ . [r]^²) (en Nm)

Après simplification.

C = k . (B₁ + (B₂. cos (q))² / (4 . P.e₀ .r) (en Nm)

· Moteurs multipolaires.

Le couple sera fonction du nombre de bobines alimentées (N_bob). Ce nombre sera pair.

Le couple C = F . rayon

C @ k .N_bob . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (8. P.e_{0 .} r) (en Nm)

Avec 0,8 <k <1

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

· Variation du couple en fonction de q, pour un bobine de stator étudiée.

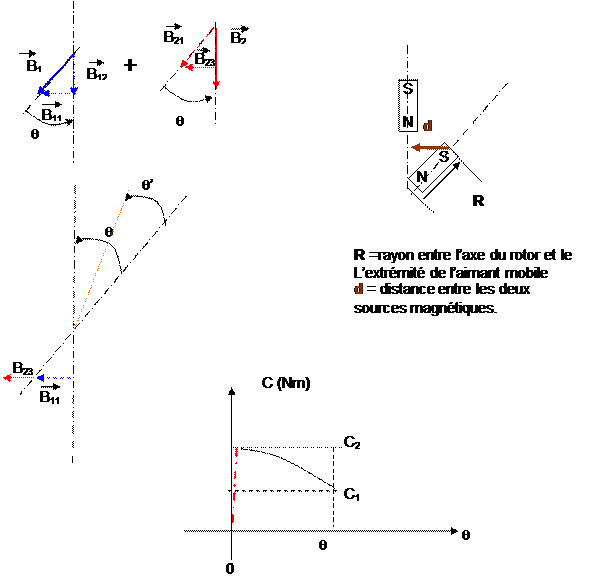
Déroulement du temps

Le couple en rotation, ne sera pas constant et va augmenter, par contre lorsque les aimants seront face à face. Il n’y aura plus de couple, ni d’attraction, ni de répulsion.

Le rotor sera littéralement collé, par une force de contact, s’il n’y a plus de changement d’alimentation de phase.

F = (B₁ +B₂)² x Surface en contact / (2 x m₀)

Avec m₀ = 4.p .10^-7 en H.m^-1

S en m²

F en Newtons

Pour une bobine seule, alimentée :

Cmoyen @ (C1 +C2)/2

@ k [(B₁ + (B₂. cos (q))² + (B₁ + (B₂. cos (0))²] / (4 . P.e_{0 .} r)/2

@ k  [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)/2

@ k  [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)

Cmoyen @ k . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)

Avec 0,8 <k <1

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

Si plusieurs bobines sont alimentées en même temps bobine seule, alimentée :

Cmoyen @ (C1 +C2)/2

@ k .N_bob . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂. cos (0))²] / (4 . P.e_{0 .} r)/2

@ k .N_bob . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)/2

@ k .N_bob . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (8. P.e_{0 .} r)

(On effectue cette approximation, car q est faible, l’erreur est minime. Par contre les fanatiques matheux peuvent et doivent dégainer leur artillerie lourde. A svoir :un calcul de moyenne, avec les intégrales)

Si l’on prend en compte des autres bobines du stator, celles-ci vont produire avec les pôles de l’aimant permanent du rotor d’autres éléments de couple.

Ceci amènera une ondulation pour le couple en fonction du temps

Un constat : Plus il y aura de bobines, plus, l’inertie nivellera le tout. Les ondulations seront rapides et de faibles amplitudes.

Force produite en contact.

Elle dépend exclusivement des intensités magnétiques de l’aimant permanent et de l’électroaimant et de la surface d’exposition.

F = (B₁ +B₂)² x Surface en contact / (2 x m₀)

avec : m₀ = 4.p10^-7H.m^-1

S en m²

F en Newtons

F = (B₁ + B₂)² x S / (2 x m₀)

3. Les moteurs pas à pas.

1. Le principe est pratiquement le même que celui des moteurs « Brusless »

· Un champ magnétique tournant est générée par des bobines fixes, alimentées séquentiellement par un dispositif électronique. Le dispositif électronique est piloté par un signal d’horloge dont la fréquence impose la vitesse de rotation du moteur.

· Le champ magnétique tournant circule au voisinage du rotor. Celui-ci va selon sa conception, être attiré, ou entrainé, ou accroché, par le champ tournant.

· Si le champs ne tourne plus, mais est maintenu, le rotor sera bloqué en une position donnée.

· S’il n’existe plus de champ du tout, alors le rotor sera libre et ne subira que des contraintes venant de l’extérieur.

2. Travail du bobineur :

Refaire si possible et à l’identique, le bobinage d’une ou de plusieurs bobines sur le stator.

Il est parfaitement déconseillé de bricoler le rotor sous peine de voir l’ensemble de dé-aimanter.

Globalement, il existe trois types matériels de moteurs.

· Les moteurs à reluctance variable. Ils ont le rotor constitué d’éléments en fer doux, qui permettent et favorise, la conduction du flux magnétique, selon les règle du flux maximum.

• Les moteurs à aimants permanents. Ils ont le rotor constitué d’une certaine quantité d’aimants permanents, ce qui génère des forces d’attraction ou de répulsion en fonction des pôles mis en présence.

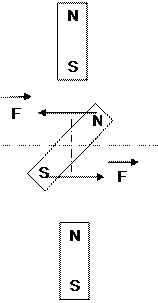
• Les moteurs hybrides. Ils combinent les deux principes précédents Ils ont le rotor constitué d’une seule paire d’aimants permanents, Par contre par un jeu de peignes on reconstitue artificiellement, le nombre de paires de pôles que l’on désire. Il est totalement déconseillé de démonter les éléments du rotor, sous peine de détruire le magnétisme.

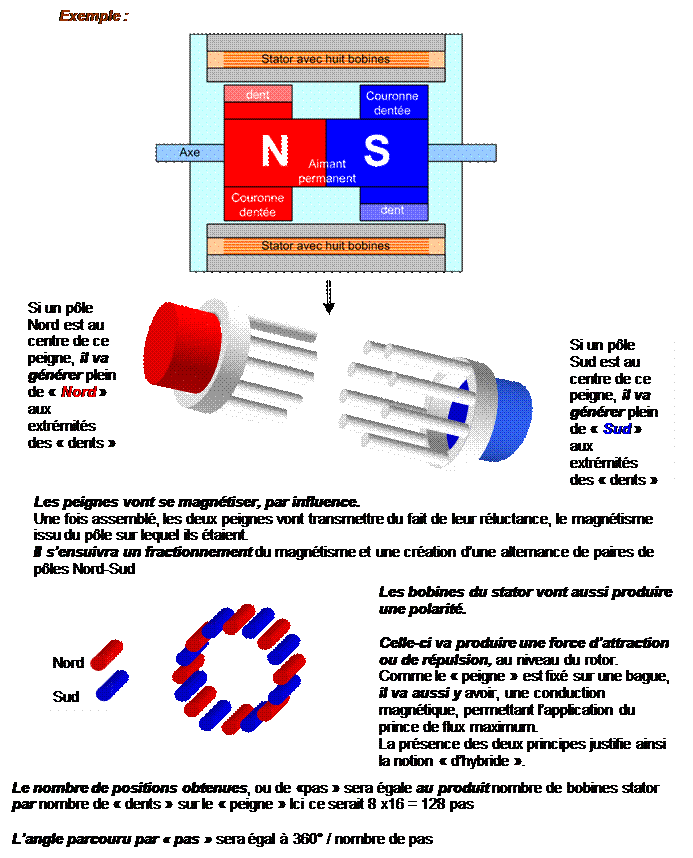
Nombres de pas = nombres bobines du stator x nombres des pôles rotor.

Angle par pas = 360 / Nombre de pas

3. La commande et l’alimentation en énergie de ces moteurs.

· Elle s’effectue grâce à un module électronique de puissance.

· Ces derniers fourniront selon les modèles, l’alimentation des bobines de phases qui produisent le champ magnétique tournant.

· Les bobines de phases sont câblées en étoile.

· L’ensemble sera cadencé avec un signal d’horloge dont la fréquence sera multiple de la vitesse de rotation.

· Il sera en général possible de changer le sens de rotation en modifiant un niveau logique, sur une entrée spécifique. Le niveau s’effectuera en TBT 1 = tension  ; 0 = absence de tension

4. La génération du champ tournant.

Selon le moteur, elle s’effectuera de 4 manières différentes.

· En pas entier, excitation normale.

Les bobines sont alimentées par paire. On permute l’alimentation dans une seule bobine à la ; le couple est optimum.

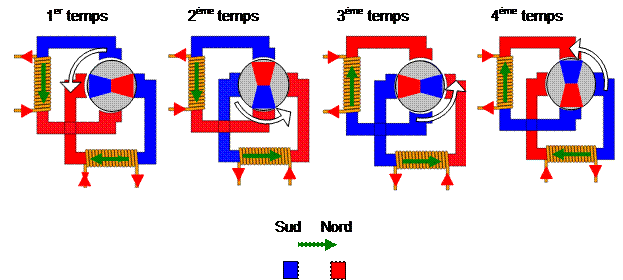
· En pas entier, excitation pleine onde

Une bobine sur deux est alimentée, le couple est deux fois plus faible, que dans les cas précédent, la puissance aussi, mais la commande est plus simple.

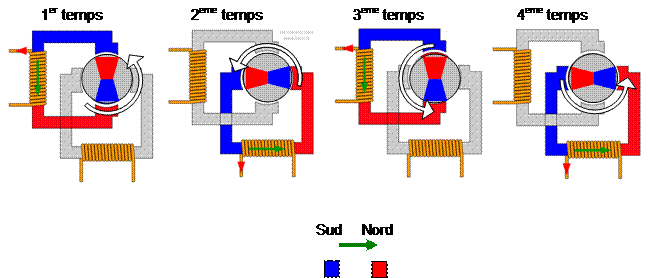
· Commande en demi-pas.

C'est une combinaison des deux modes précédents.

Le rotor se déplacera, demi-pas, par demi-pas, la vitesse sera la moitié de celle constatée dans les deux cas précédents.

La puissance et le couple seront intermédiaires aux moteurs précédents.

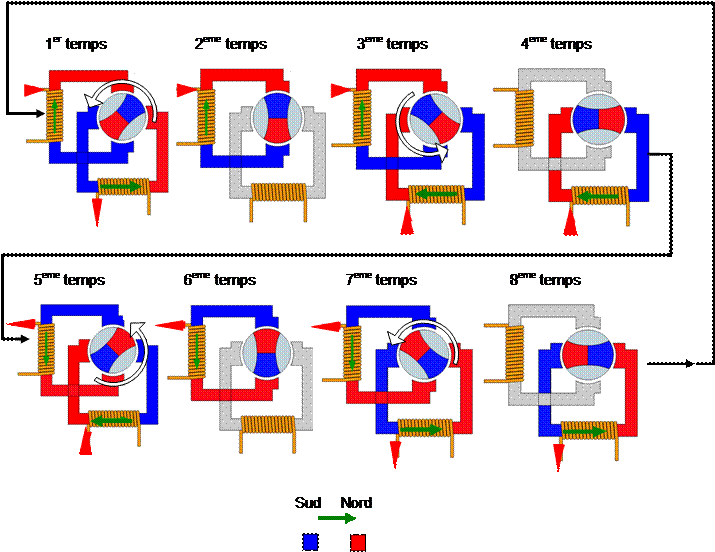
· Commande en micro pas.

Les bobines seront alimentés avec des courants analogiques variables identiques en formes, mais déphasés d’un angle égal au décalage existant entre les deux bobines.

Les courants sont généralement de l’alternatif sinusoïdal.

Ces deux courants vont induire un champ magnétique tournant, dont l’étude plus approfondie donnerait la relation bien connue des électriciens bobineurs :;

f _{fréquence en Hertz} = p _{paires de pôles} . n _{vitesse de synchronisme en tours /secondes}

Si la fréquence est asservie au démarrage du moteur par un module électronique, on obtient au final, une machine synchrone !

Si la fréquence n’est pas asservie, le moteur « démarre comme, il peut », c'est-à-dire :

· si le couple au démarrage est trop faible, le rotor, ne pourra pas accrocher le champ tournant. Le moteur ne démarrera pas !

· S’il démarre, la vitesse va se stabiliser.

Au final on obtiendra encore, une machine synchrone

Un exemple :

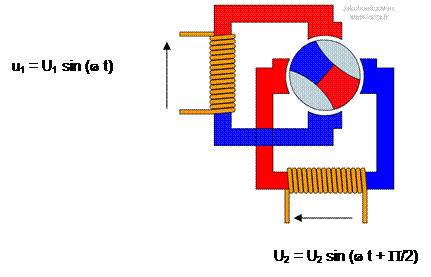
f = p . n

p = 2 paires de pôles

Si f = 50 Hz

Alors, n = 50 / 2 = 25 tours/ seconde =1500 t / minute

5. Calculs des bobines.

Travail du bobineur :

Refaire si possible et à l’identique, le bobinage d’une ou de plusieurs bobines sur le stator.

Il est parfaitement déconseillé de bricoler le rotor sous peine de voir l’ensemble de dé-aimanter.

S’il faut, quelques théories, ou « Comment calculer le bobinage ? »

Tension nécessaire pour une bobine inductrice.

b) Il faudra connaître les deux inductions magnétiques mises en jeu ou possibles.

· B₁ dépendra du châssis magnétique choisi. Il faudra connaître le maximum possible sans saturation et de la bobine de phase. Il existe une méthode sur le site « Mistershoeélec » en catégorie « bobinage ».

· B₂ sera fixe et dépendra des aimants permanents.

E = N.(B₁+ B₂). Lo . n . 2P. R

Avec :

E = tension maximum imposée à la bobine inductrice.

dx/dt = vitesse tangentielle de rotation de l’aimant permanent = n . 2P. R

n = vitesse de rotation de la partie mobile, en tours par seconde.

N = nombre de spires

Lo = longueur de bobine, en m.

R = Rayon du rotor ou de la roue polaire, en m

Ce qui sera suffisant par un technicien souhaitant calculer un nombre de spires

Intensité dans une bobine.

· I moyen = E.T/L/2

· Si l’on veut I efficace, pour la section des fils = E.T/L/ 1,414

L = coefficient d’auto induction d’une bobine :

L = ( μ₀ . μ_r . N² . S _{surface de la bobine}) / L _{longueur de la bobine} (si μ₀ et μ_r sont connus)

Sinon, la bobine possédera un coefficient L donnée qu’il est possible de mesurer par une méthode « voltampèremétrique », en alternatif, et continu, par la méthode des impédances.

Pour trouver Z = U _continu / I _continu pour avoir R,

Pour trouver Z = U_alternatif / I _alternatif et continu, par la méthode des impédances.

L = Racine carré de (Z² -R²)/2π.f

Ce qui sera suffisant par un technicien souhaitant calculer un nombre de spires et la section.

Puissance absorbée d’une bobine.

Pmoyen = U moyen . I moyen = E . E.T/L/2

Remarque : Il faudra connaître le mode de fonctionnement du module d’alimentation pour savoir le nombre de bobine alimentée en même temps. Ceci permettra de calculer la puissance totale, absorbée par le moteur.

P_utile (Watts) = 2 . P .n .C ≈ P_absorbée (au rendement près)

Sinon, au pire le rendement sera égal à 80 %

Ce qui donnerait, P_utile (Watts) = 2 . P .n .C/ 0,8

Avec n = vitesse de rotation en tours/secondes = K . f

(f = fréquence de commande du module d’alimentation des phases du moteur.)

Force de contact.

Elle dépend exclusivement des intensités magnétiques de l’aimant permanent et de l’électroaimant et de la surface d’exposition.

F = (B₁ + B₂)² x Surface en contact) / (2 x m₀) ¹

Avec : m₀ = 4.p10^-7 en H.m^-1

S en m²

F en Newtons

F = (B₁ x B₂ x S) / (2 x m₀)

Vérification des formules :

1. Pour E (Volts)

Nous aurons pour une bobine :

E= N. dΦ/dt

Avec Φ (flux magnétique = B x surface), qui dépendra de B₁ et B₂ et de la surface mise en exposition de magnétisme.

La surface va varier, avec la rotation

· B₂ est produit par un aimant permanent.

· B₁ est produit par une bobine « longue »

C'est une bobine beaucoup plus longue que large. Elle se nomme solénoïde. Elle comporte plus d'une spire et dont l'induction en son centre vaut :

B1 = μ₀ . μ_R . N . I / L_B

Avec :

μ₀ = Perméabilité relative de l’air = 4 .π ; 10^-7

μ_r = Perméabilité relative du matériau.

N = nombre de spires

(Il n’est pas forcement nécessaire de connaître ces valeurs, il est possible de les mesurer.)

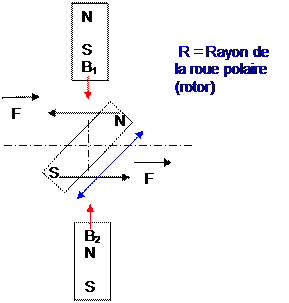
E = N. dΦ/dt deviendra N .d (B₁+ B₂ ). Lo . dx/dt

E = N . dj/dt = (B₁+ B₂ ). Lo . dx/dt

Avec :

E = tension maximum imposée à la bobine inductrice.

dx/dt = vitesse tangentielle de rotation de l’aimant permanent = n . 2P. R

n = vitesse de rotation de la partie mobile, en tours par seconde.

N = nombre de spires

Lo = longueur de bobine, en m.

R = Rayon du rotor ou de la roue polaire, en m.

La formule deviendra :

E = N . dj/dt = (B₁+ B₂ ). Lo. dx/dt = N . dj/dt = N . (B₁+ B₂). Lo . n . 2P. R

E = N.(B₁+ B₂). Lo . n . 2P. R

Ce qui sera suffisant par un technicien souhaitant calculer un nombre de spires.

2. Pour I moyen dans une bobine I (Ampère)

i en fonction du temps dans une bobine.

Le solénoïde  aura pour coefficient d’auto induction L = N . d j / d i _{(dans la bobine)}

L = coefficient d’auto-induction d’une bobine, en Henry = μ₀.μ_r N²/ longueur du soleinoïde

L, en Henry

Avec : d j =(B₁+ B₂ ). Lo. dx

μ₀ = Perméabilité relative de l’air = 4 . π .10^-7

μ_r = Perméabilité relative du matériau.

N = nombre de spires

Et e(V) = N . dj/dt = L di/dt

Ce qui amènera :

E = N .(B₁ + B₂). Lo . n . 2P. R = L di/dt

Ce qui implique que si E est brutalement appliqué et constant (ainsi que B₁, B₂), i sera de forme affine (c’est un calcul intégral)

Tel que i (t) = E . t / L

I va progresser le temps d’alimentation d’une bobine et aura la forme suivant.

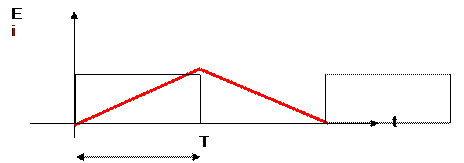
T sera le temps d’alimentation d’une bobine. Ce temps sera fonction de la fréquence de pilotage du module d’alimentation du moteur. Ce temps dépendra aussi de la commande désirée, en pas entier, demi-pas, etc.

La bobine possédera un coefficient L donnée qu’il est possible de mesurer par une méthode « voltampèremétrique », en alternatif, et continu, par la méthode des impédances.

Pour trouver Z = U _continu / I _continu pour avoir R,

Pour trouver Z = U_alternatif / I _alternatif et continu, par la méthode des impédances.

L = Racine carré de (Z² -R²)/2π.f

Si l’on veut calculer à condition de posséder les coefficients…

L = ( μ₀ . μ_r . N² . S _{surface de la bobine}) / L _{longueur de la bobine}

Avec :

μ₀ = Perméabilité relative de l’air = 4 .π ; 10^-7

μ_r = Perméabilité relative du matériau.

N = nombre de spires

D’après la courbe de i(t)

I mini = 0

I maxi = E.T/L

Donc I moyen = E.T/L/2

Si l’on veut I efficace, pour la section des fils = E.T/L/ 1,414

(I efficace (racine carrée de i² moyen),

Ce qui sera suffisant par un technicien souhaitant calculer la section des spires.

3. Calcul du couple en fonction du temps.

L’approche est analogue à celle des moteur « Brusless » par contre le rayon, est moindre.

· Moteurs avec une seule bobine seule, alimentée :

Le couple total sera égal F fois l’écart entre l’application de la force et le rayon du rotor,

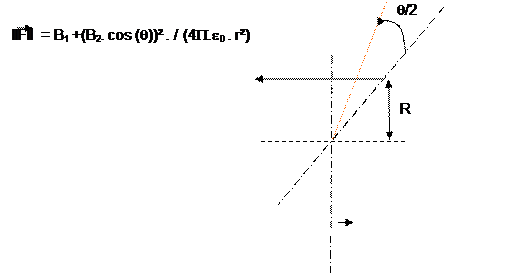
Le couple C = F r

= k . (B₁ + (B₂. cos (q))² .r / (4P.e₀ . [r]^²) (en Nm)

Après simplification.

C = k . (B₁ + (B₂. cos (q))² / (4 . P.e₀ .r) (en Nm)

· Moteurs multipolaires.

Le couple sera fonction du nombre de bobines alimentées (N_bob). Ce nombre sera pair.

Le couple C = F . rayon

C @ k .N_bob . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (8. P.e_{0 .} r) (en Nm)

Avec 0,8 <k <1

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

· Variation du couple en fonction de q, pour un bobine de stator étudiée.

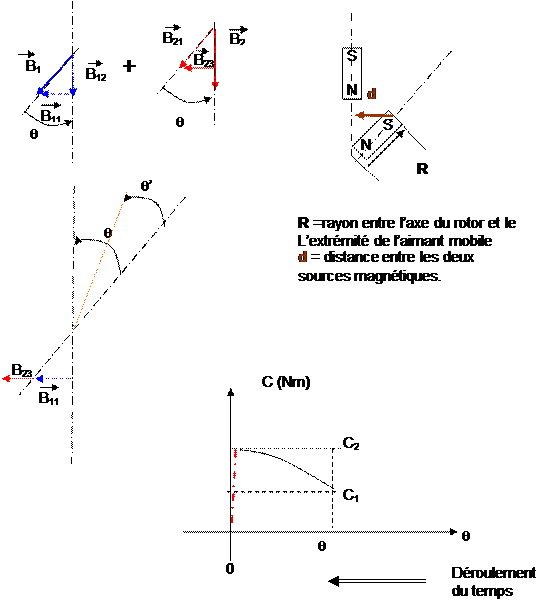
Le couple en rotation, ne sera pas constant et va augmenter, par contre lorsque les aimants seront face à face. Il n’y aura plus de couple, ni d’attraction, ni de répulsion.

Le rotor sera littéralement collé, par une force de contact, s’il n’y a plus de changement d’alimentation de phase.

F = (B₁ +B₂)² x Surface en contact / (2 x m₀)

Avec m₀ = 4.p .10^-7 en H.m^-1

S en m²

F en Newtons

Pour une bobine seule, alimentée :

Cmoyen @ (C1 +C2)/2

@ k [(B₁ + (B₂. cos (q))² + (B₁ + (B₂. cos (0))²] / (4 . P.e_{0 .} r)/2

@ k  [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)/2

@ k  [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)

Cmoyen @ k . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)

Avec 0,8 <k <1

K reste le coefficient réducteur lié à l’écartement et à la forme des sources magnétiques.

Si plusieurs bobines sont alimentées en même temps bobine seule, alimentée :

Cmoyen @ (C1 +C2)/2

@ k .N_bob . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂. cos (0))²] / (4 . P.e_{0 .} r)/2

@ k .N_bob . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (4 . P.e_{0 .} r)/2

@ k .N_bob . [(B₁ + (B₂. cos (q))² + (B₁ + (B₂.)²] / (8. P.e_{0 .} r)

(On effectue cette approximation, car q est faible, l’erreur est minime. Par contre les fanatiques matheux peuvent et doivent dégainer leur artillerie lourde. A savoir : un calcul de moyenne, avec les intégrales)

Si l’on prend en compte des autres bobines du stator, celles-ci vont produire avec les pôles de l’aimant permanent du rotor d’autres éléments de couple.

Ceci amènera une ondulation pour le couple en fonction du temps.

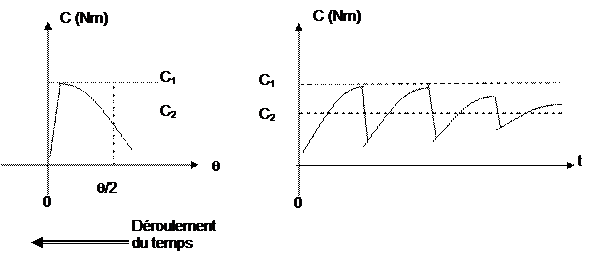
Un constat : Plus il y aura de bobines, plus l’effet de l’inertie, nivellera le tout. De même la fréquence d’alimentation des bobines va jouer et plus celle-ci sera forte, plus le couple tendra à être constant. La conjonction des deux effets fera que les ondulations seront rapides et de faibles amplitudes.

Retour