Comment connaître l’induction maximale pouvant circuler dans un circuit magnétique alternatif, ou comment éviter la saturation magnétique.

 

 

Préambule :

 

Il n’existe pas (à ma connaissance) de méthode théorique avec un modèle de bobine ou d’électroaimant, avec des composants de base R, L, C, constants.

 

En effet un électroaimant va voir ses caractéristiques évoluer en fonction de la température, la saturation magnétique du noyau, des matériaux, etc.

Il existe bien un modèle (de Kapp) faisant intervenir les pertes par effet joules dues aux courants directs et aux résistances des différentes bobines, les pertes par les courants de Foucault, les effets des mutuelles inductances, mais, pour ces deux derniers, les composants fictifs choisis sont variables en fonction des courants et des magnétismes produits et demandés.

 

De même, ces composants imaginés ne sont pas linéaires dans le temps, ils tiennent compte de la rémanence magnétique (persistance de l’aimantation dans un barreau), de la fréquence.

 

Si l’on ne possède pas une banque de données pour un type de matériaux données, dans une situation particulière, il sera impossible de prévoir les réactions d’un circuit magnétique. Il faudra essayer, voir les résultats et corriger pour réessayer.

 

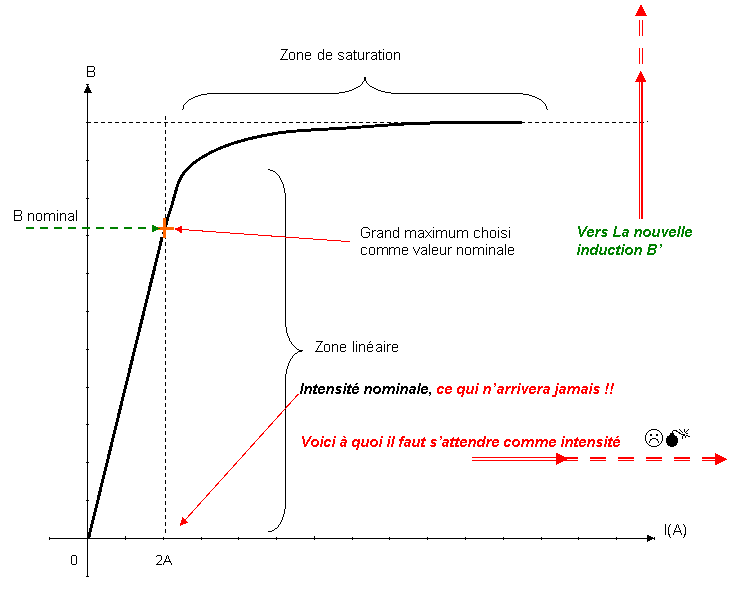
Par contre, il existe une méthode simple pour mesurer facilement. Les résultats se présentent sous la forme d’une courbe de première aimantation. Avec seulement, une zone linéaire et une zone de saturation.

 

Si l’on doit se souvenir que d’une chose :

 

Il ne faudra jamais travailler en zone de saturation !

 

 

 

Les avantages :

 

• Les résultats sont sans ambiguïtés.
• Le travail se fait en alternatif. Les résultats sont indépendants des phénomènes de rémanence et de coercition magnétique.
• La méthode est applicable quelque soit la fréquence du réseau (50, 60, 600 Hz…)
• Les mesures sont simples à réaliser.
• Il faut réaliser un mini transformateur. Dans le cas de moteurs asynchrones, il est possible de conserver les modèles réalisés, car un professionnel du bobinage, devra travailler souvent sur des modèles identiques de châssis. Ce type de mini transformateur est facile à réaliser.
• Il faudra un alternostat pour faire varier la tension d’alimentation, un ampèremètre, un voltmètre,  du papier blanc et une feuille millimétrée pour relever les mesures, une calculatrice et un cerveau pour interpréter.

 

Les inconvénients :

 

• Il faut, au cas par cas, réaliser un mini transformateur, avec un primaire et un secondaire, dont les bobinages seront adaptés à la zone, où passera le magnétisme. Si l’on doit changer souvent de support, il faut refaire un transformateur.
• Il faut parfois faire des calculs de surface complexes.

 

I.      Comment faire ?

 

1. Il faut connaître le schéma de bobinage à réaliser, dans sa forme la plus générale.

 

2. Il suffit de réaliser un mini transformateur abaisseur de tension (tension du secondaire plus faible que celle du primaire)

·         Dans le cas d’un moteur asynchrone, il suffit de réaliser un gabarit de bobine, comme si l’on connaissait le nombre de spires d’une petite section. La surface importe peu, mais, il est préférable de choisir des dimensions proches de celles prévues pour la plus petite bobine

 

Il faudra placer cette réalisation dans les encoches  d’un châssis ou d’un rotor.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

·         Dans le cas d’un transformateur, il faut sacrifier un support.

 

 

 

 

 

 

 

 

 

 

 

Il faudra insérer les lames du circuit magnétique, comme si l’on réaliser réellement le transformateur.

 

3. Les deux bobinages seront distincts.

·         Celui qui servira de primaire devra avoir un nombre conséquent de spires. Au moins, une centaine.

·         Pour le secondaire, une dizaine ou deux suffiront.

 

L’essentiel est de connaître exactement le nombre de spires dans les deux bobinages !

 

4. Le montage expérimental suivant sera réalisé :

·         Variante avec pince ampéremétrique.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

·         Variante avec ampèremètre de laboratoire.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

En agissant sur l’alternostat, il sera possible de faire varier la tension du primaire et par-là même, l’intensité du primaire.

Le secondaire suivra les variations en tension du primaire.

 

 

5. L’alternostat devra être placé en position minimum. Il faut bien vérifier de commencer à 0 Volts. Peu à peu la tension du primaire sera augmentée. Il faudra relever des groupes de  valeurs U₂ et I₁ (une dizaine au minimum) en prenant garde que l’intensité ne devienne pas destructrice.

 

6. Les résultats seront notés de façon à tracer du mieux possible la courbe U₂ = f(I₁) correspondante.

 

7. Il sera mathématiquement démontré par la suite, que :

 

·         L’induction B maxi, se calculera ainsi :

 

 

 

Car U₂ est une image de l’intensité magnétique ( B) circulant dans le châssis à tester.

 

Avec :

·         U₂ est la tension efficace relevée au secondaire du  mini transformateur

·         S = surface en m²

·         f = fréquence en Hz.

·         N₂ = nombre de spires connues au secondaire du transformateurs réalisé

 

Remarque : il serait totalement possible de mesurer U1 et de faire les calculs avec N1. Cependant, en pratiquant ainsi, on est sur que du magnétisme se produit dans le support et l’on travaille avec plus de sécurité en basse tension

 

 

·         L’intensité I₁ ne sert pas au calcul, mais permet de tracer la courbe il sera possible de voir en quel lieu commence la saturation magnétique.

 

La valeur de B max sera ainsi estimable !

 

 

·         Pour être complet, le produit : I₁ x le nombre de spires primaire N₁ correspondra au nombre d’Ampéres-tours nécessaires pour obtenir B.

II.      Un exemple complet.

Monsieur « Z » de la société « Y » reçoit un moteur à rembobiner. Il n’est pas content, car le moteur était tout grillé et son apprenti, croyant lui faire plaisir a tout retiré à l’intérieur. Toutes les informations

 

Il commence par tuer son apprenti.

 

Les données nécessaires à la reconstruction du moteur : bobinages, connexion, nombre de spires sont perdues !

Machine et  apprenti, sont partis au paradis des moteurs !

 

Il n’a pas Internet ou bien la société qui a construit le châssis, est fermée depuis longtemps !

Il ne sait que la tension d’usage du moteur et le réseau  (triphasé ou monophasé) à 50 Hz.

Il a appris, il y a longtemps, comment trouver le schéma de bobinage et calculer le nombre de spires.

Par contre, il lui faut l’induction maximale qui peut passer dans le châssis.

 

1. Il réalise un schéma et voit comme devraient être disposées les sections.

 

2. Il fabrique un gabarit de bobine, il en profite pour savoir la surface de la bobine

(0,2 x 0,05 = 0,01 m²)

 

3. Il y a 100 spires au primaire et 10 au secondaire.

 

4. Il réalise la manipulation décrite. Et trace une courbe du mieux qu’il peut (bien !)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5. Monsieur « Z » choisit  18,5 V comme tension avant la saturation.

 

 

 

 

6. Connaissant B Maxi, il sera possible pour lui de calculer le nombre de spire de son moteur.

 

Pour l’exemple choisi qui n’est pas forcément représentatif de la réalité…… (On ne doit pas tuer son apprenti !)

III.      Pour ceux qui aiment les mathématiques appliquées.

 

D’où vient la méthode ?

 

Des lois relatives au magnétisme ; plus particulièrement celles de Lenz, sur le flux magnétique et de l’induction des courants.

 

Si un conducteur est soumis à une variation de flux dans le temps, il va induire un courant. Le sens du courant induit sera tel que les effets produits par ce courant, tendront à s'opposer à la cause de qui lui a donné naissance.

 

L'induction du courant se produira, tant que durera la variation de flux.

 

S'il y a plusieurs conducteurs enroulés, le flux total va augmenter du nombre de spires constatées.

 

Lenz a tiré une formule :

Où :

• N est le nombre de spires de fils.
• F(t) est l’expression du flux magnétique en fonction du temps, en gros :

 

F(t) = Intensité magnétique (B, en Teslas) en fonction du temps x Surface (en m²)

 

F(t) = B(t) x S

 

• signifie : dérivée du flux magnétique par rapport au temps.

 

 

Pour un transformateur, les nombres de spires seront différenciés Par N₁ (primaire) et N₂ (secondaire) ; si l’on se place  au secondaire nous aurons :

 

 

L’expression pourrait se mettre sous la forme :

 

 

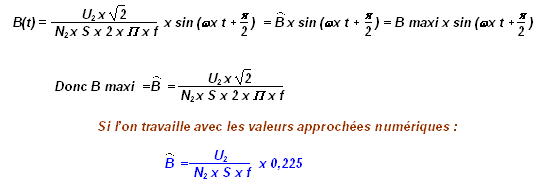
Avec :

·         U₂ est la tension efficace relevée au secondaire du  mini transformateur

·         S = surface en m²

·         f = fréquence en Hz.

·         N₂ = nombre de spires connues au secondaire du transformateurs réalisé

 

 

Remarque : il serait totalement possible de mesurer U1 et de faire les calculs avec N1. Cependant, en pratiquant ainsi, on est sur que du magnétisme se produit dans le support et l’on travaille avec plus de sécurité en basse tension

 

 

 

En ce qui concerne la génération de l’intensité magnétique par rapport  à l’intensité i (t)

 

B (t) et donc aussi F (t) est directement fonction de i (t)

 

Telle que  F (t) = B(t) x S

 

F (t) = K x i

 

K sera :

·         Linéairement fonction du nombre de spires, de la longueur de la bobine, de sa section, de l’intensité i et de la perméabilité magnétique du vide m₀ =  4 x p x  10^-7

·         Pas du tout linéairement fonction, de la perméabilité relative du noyau ferreux utilisé (m_R)

 

Ce n’est pas grave, car cela nous permettre de visualiser ainsi les phénomènes de saturation magnétique, sur la courbe U₂ = f(I₁) ou B = f(I₁)

Cette intensité ne servira qu’à magnétiser les matériaux.

 

 

IV.      Pourquoi ne pas travailler en saturation ?

 

Pour une raison de consommation d'intensité !

(Généralement pas du tout prévue)

 

1. Lorsque l’on raisonne en tension, le magnétisme est directement imposé par la tension.

 

 

Si e augmente, F aussi et dans les mêmes proportions.

 

2. Lorsque l’on travaille en courant, il faut augmenter l’intensité pour que le magnétisme croisse.

En zone de saturation, l’augmentation de I doit être plus importante pour obtenir une variation minime de l’induction.

 

3. Deux cas peuvent se présenter :

·         Le bobinage est bien conçu, L’intensité nominale est, par exemple de 2A. Pour une raison « X », la tension d’alimentation  augmente beaucoup, du double par exemple.

Si U double B aussi, donc il faudra une intensité I énorme pour arriver à cela.

Cette intensité s’apparentera à un court-circuit !

 

 

 

 

·         Le bobinage est mal conçu  : L’intensité nominale devrait être, par exemple de 2A. et la tension beaucoup plus faible.

 

Mis en situation normale, tout va se passer comme si la tension d’alimentation avait brutalement augmentée, de beaucoup, du double, du triple...

 

Si U double, triple, alors B aussi, donc il faudra une intensité I énorme pour arriver à cela.

Cette intensité s’apparentera à un court-circuit !