Alternatif sinusoïdal

1.    Notions de base  :

-    Un courant alternatif est un courant périodique de valeur moyenne nulle.

-    Sa fréquence se calcule en effectuant le rapport 1/ T

 2.    Courant alternatif sinusoïdal. 

    3.    Tracé d’une sinusoïde.

 4.      Représentation de Fresnel.

 Chaque expression de grandeurs sinusoïdale peut-être représentée sous la forme suivante :

-          u1 = Û1 . sin (w.t + j1 )

-          u2 = Û2. sin (w.t + j2 )

-          u3 = Û1 . sin (w.t + j1 )

 Chacune des expressions peut-être ramenées à un vecteur représentatif ayant une norme et un déphasage j. Le déphasage est calculé par rapport à l’axe des origines.

            Ainsi pour u₁ :                II Û₁ II avec j₁.

            Ainsi pour u₂ :                II Û₂ II avec j₂

            Ainsi pour u₃ :                II Û₃ II avec j₃.       etc.…

Remarque : la mesure des angles s’effectue selon le sens trigonométrique et relativement par rapport soit à l’axe des origines, soit par rapport à un vecteur pris pour référence.

         Exemples :

                a ) Déphasage nul.

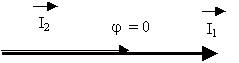
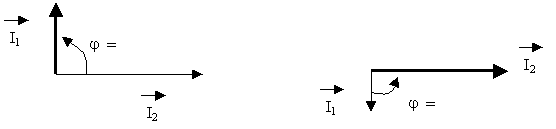
                b ) Courants en opposition

        c) Courant en quadrature 

            Se dit lorsque les déphasages égalent + ou - pi/2

5.      Somme ou différence de grandeurs sinusoïdales.

A) Théorème de Fresnel : 

Il est possible de trouver le résultat d’une somme ou d’une différence de toutes expressions sinusoïdales de même fréquence en effectuant la somme ou la différence vectorielle des vecteurs caractéristiques des expressions. 

-         Donc, s’il faut effectuer :      Û₁ . sin (w.t + j₁ ) + Û₂. sin (w.t + j2 ) 

   Le résultat sera de la forme  u_T = Û_T . sin (w.t + j_X ) tel que :

 
                           Û_T = Û₁ + Û₂

Remarques :  

-  Il est possible d’utiliser la règle pour plus de deux vecteurs de Fresnel.

-  Dans les cas où, les déphasages sont égaux à 0, + pi / 2 ou - pi /2, 

le théorème de  Pythagore peut s’appliquer.   

B )Théorie sur les complexes.

Elle est basée sur une exploitation  des principes vectoriels associé à l’usage de l’algèbre. Ce dernier s’utilise pour calculer les positions des coordonnées des points essentiels des vecteurs utilisés.

                                                                ( origine et fin)

Les complexes utilisent une représentation axiale spéciale :

         -         L’axe des ordonnées est nommé, axe des imaginaires et est associé

                    à une variable « j ».

  -         L’axe des abscisses est nommé : axe des réels.

  -         Tout nombre complexe est déclaré par une lettre associée à une barre

            en dessous :  C.

  -         Un nombre complexe s’écrit sous la forme a + j . b

  -        Toutes rotation d’un angle de pi /2 entraîne une multiplication du

            nombre complexe par « j ».

  -         Le produit j. j = j² =  - 1

  -        Tout nombre complexe est caractérisé par son module ( r ) et son

            argument ( q ).

  -         Le module correspond à l’intensité du vecteur  traité.

  -         L’argument correspond à l’angle constaté par rapport à l’axe des réels.

 Exemple :

Compléments mathématiques :

            -      Nombre complexe conjugué : si c =a + jb, le conjugué de c = a - jb   

-         Expression canonique :  si c =a + jb, c peut s’écrire c = r ^q ou r.^{e jq}   

-       Règles des produits de nombres complexes : C1 . C2 = tel que :

  r = r 1 . r2 et q = q1 + q2   

-       Règles des rapports de nombres complexes : C1 / C2 = tel que :

 r = r 1 / r2 et  q = q1 - q2

Expression complexe des composants R, L, C en  alternatif.

        Remarque : 

 Toutes les applications possibles en électricité des nombres complexes sont régies par les lois générales. Dans le cas de l’utilisation des impédances complexes d’éléments, on parlera et l’on traitera en premier de manière générale, par les impédances Z_R, Z_C, Z_L. Au besoin un schéma des impédances sera fait. En dernier, une identification des différentes  impédances sera faite.

Retour