Application des complexes à la résolution de filtres en alternatif.

 1.     Définition d’un filtre

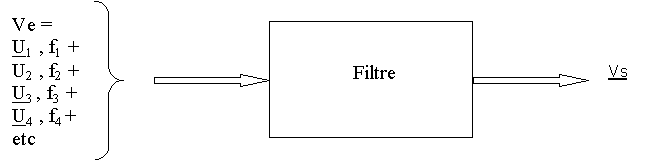
  Un filtre est un quadripôle utilisé en alternatif qui permet de favoriser ou au contraire atténuer certaines composantes alternatives d’une source de tension.

Il est possible de représenter la réponse des filtres par un système d’axes linéaires ou semi-logarithmiques. Il existe deux types fondamentaux de filtres :

         -       Les filtres passes bas, qui favorisent les basses fréquences et atténuent les hautes.

       -       Les filtres passes hauts, qui réalisent l’inverse.

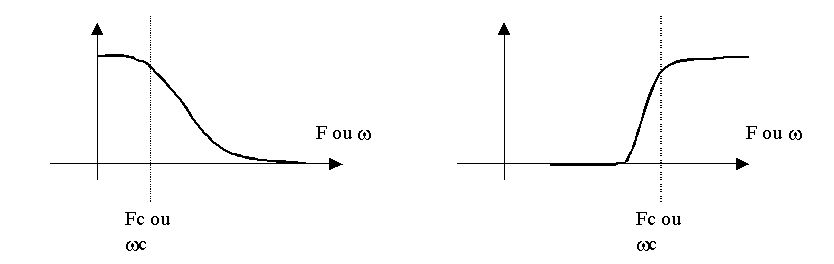Remarque :

-       Fc ou fréquence de coupure se mesure et se calcule lorsque Vs = Ve /

-       L’argument s’exprime de Vs vers Ve.

-       Il existe des filtres qui combinent les deux effets et qui se nomment : Passe-bande ou coupe- bande.

2.     Calcul de filtre.

Le calcul et l’analyse de filtre peut être assez difficile. Nous utiliserons les nombres complexes associés au lois générales de l’électricité.  

        Procédure : 

1.   Tout s’effectuera au préalable par l’établissement d’un schéma des impédances.

2.   Expression de Vs en fonction de Ve, à partir du schéma des impédances.

3.   Identification des impédances complexes.

4.   Calcul des limites de Vs et de q, en fonction de w.

5.   Calcul de Vs et de q, en fonction de wc ou fc.

6.   Établissement d’un tableau de variation  du module de Vs (éventuellement de l’argument) en fonction de w ou de f.

7.   Tracé, si nécessaire de II Vs II = F (w)

         Remarque : 

La notion d’ordre d’un filtre dépendra de l’exposant  de, qui se trouvera dans les dernières équations simplifiées de Vs en fonction de Ve.

                 -       Ordre 1 :                      présence de (w.j)

                 -       Ordre 2 :                      présence de (w.j)²

                 -       Ordre 3 :                      présence de (w.j)³

 Nous ne dépasserons pas l’ordre 2 du fait des grandes difficultés à traiter des puissances supérieures.   

3.     Une application. 

     Filtre passe bas R.C.

              Rappel : un filtre passe-bas est un quadripôle qui atténue les composantes d’un signal reçu sur son entrée à partir d’une fréquence nommée fc.

           1 ) Soit le circuit suivant :  

           2 )       Vs = ? avec le schéma des impédances.                            

             3 )       Identification des impédances

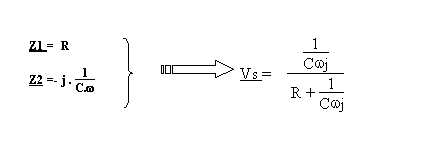
                En multipliant, numérateur et dénominateur par Cwj nous obtenons :

            4)     Calcul des limites

lim de Vs si w tend vers 0 = Ve                    lim de q si w tend vers 0 =  - arctang (RCw ) = 0

lim de Vs si w tend vers ¥ = 0                      lim de q si w tend vers ¥ = - arctang (RCw ) = - pi / 2

        5)     Calcul de Vs si w = wc   ( dans ce cas RCwc  = 1)

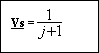
        6)     Variation du module de Vs

         7)        Tracé de Vs = F (w)

Retour