 |
Nous nous bornerons à une étude spécifique des puissances mises en jeux avec du courant alternatif de fréquence fixe.
Le calcul
de puissance s’effectue en faisant la moyenne du produit des valeurs instantanées
de la tension par l’intensité. La puissance dite active est
celle qui est capable d’effectuer un travail dans un temps donné. Elle
permettra de choisir les caractéristiques des composants : section des
fils, largeur des pistes, puissances normalisées supportables etc.
P ( moyenne ) = ( u .i ) moyen.
Si nous avons affaire à des courants sinusoïdaux déphasés, cette puissance active n’est pas forcément égale à P =U . I.
La
puissance dépendra du déphasage
constaté de I vers U .
Exemples
types :
-
Pour un résistor : q
= 0 rd.
P = U . I
 |
-
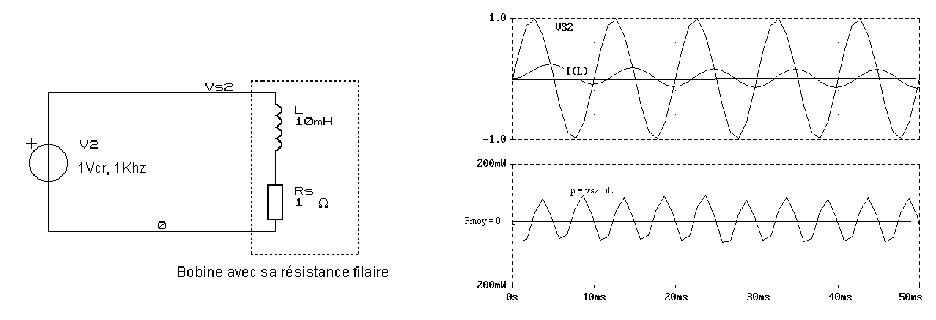
Pour une bobine : q
= pi / 2
rd.
, avec pi =
3.14
P
¹
U . I
 |
- Pour un condensateur le déphasage est : q = -pi /2 rd.
L’opposé de celui d’une bobine. Le calcul de p moyenne nous amènerait à constater que p moy = 0, donc :
P ¹ U . I
Une
étude mathématique utilisant les calcul intégral permet de déterminer la puissance active consommée par un récepteur
en fonction du déphasage. Il permet en outre de déterminer deux autres
puissances résultantes.
-
Puissance active :
P = U
.I . cos ( q
)
-
Puissance réactive :
Q = U . I . sin ( q
)
-
Puissance apparente :
S = U . I ou S² = P² +
Q²
Remarque : la puissance apparente peut s’exprimer sous
forme complexe :
S =
P + jQ
Soit un observateur placé face à miroir, le soleil est derrière lui.
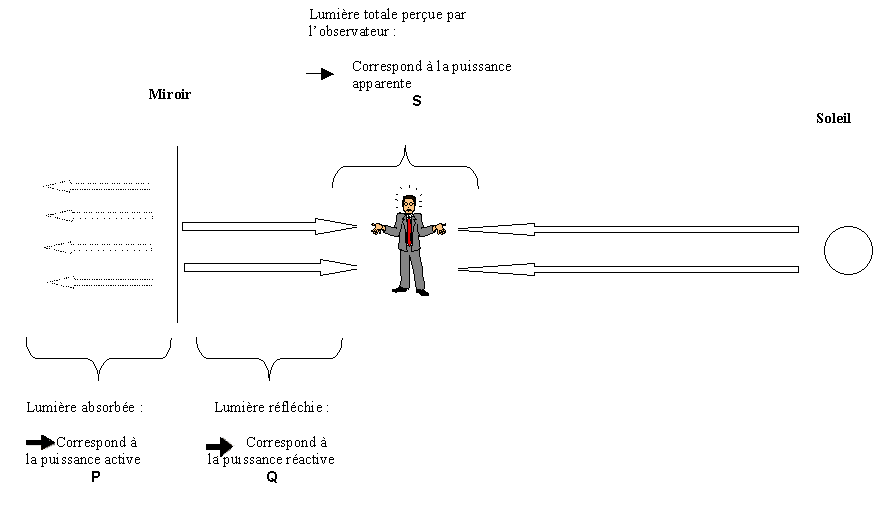 |
Remarque :
La puissance réactive est fournie par le générateur et est réfléchie par le
récepteur vers le générateur, son importance dépend du déphasage produit
par le récepteur. Elle n’est pas perdue, mais le transfert provoque
quand même des pertes par effet Joules.