- Le courant triphasé est produit par une machine tournante qui produit
de l’énergie électrique. Elle se nomme alternateur.
- Elle est composée de trois bobinages fixes disposés sur un cylindre
et disposés l’un de l’autre à 120°.
- Chaque bobinage a une de ses sorties réunie en un point nommé « Neutre ».
- La sortie qui reste est nommée « Phase ».
- Au centre du cylindre tourne une série d’aimants.
- Les trois tensions produites se nomment tensions simples :
V1N, V2N, V3N.
 |
|
- Chaque
pôle magnétique tourne au voisinage de chaque bobine. - La
variation de flux magnétique va induire dans chacune une f.e.m (Loi de
LENZ). - Les
fems seront alternatives car la variation de flux est alternative (Nord,
Sud, Nord, Sud…) -
Chacune
des bobines va voir à son tour passer un pôle Nord , les fems seront
donc déphasées. - Comme les bobines sont décalées de 120°, le déphasage des fems sera de120°. |
 |
- Soit le schéma de montage suivant :
 |
Remarques :
- A n’importe quel moment, il y a toujours deux tensions de même signe.
- En France, le secteur est compris entre 220V et 240V efficace, pour 50Hz.
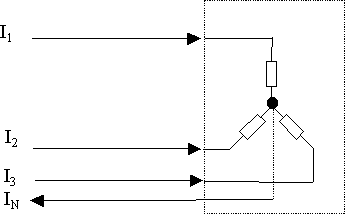
- Il est possible d’utiliser les trois phases et le même neutre en même temps. Le montage est appelé « étoile »
- Dans ce cas, les intensités se positionnent ainsi :
 |
 |
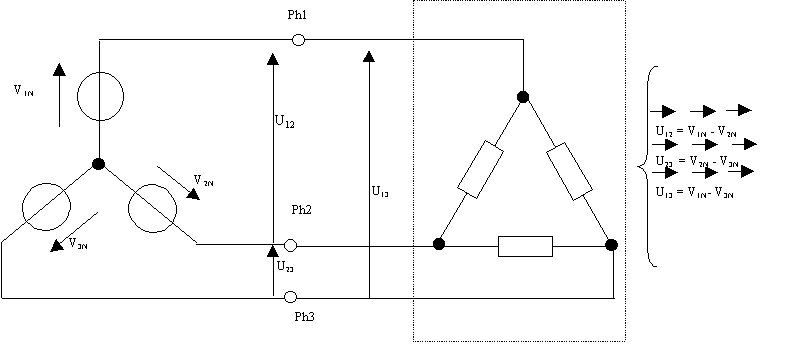
Il est possible d’utiliser les trois phases sans le neutre. Le montage est appelé « triangle ».Chaque récepteur est connecté entre deux phases.
Les tensions obtenues se nomment « tension composées » et sont égales, de part la loi des mailles, à la différence de deux tensions simples.
A n’importe quel moment, il y a toujours deux tensions de même signe.
 |
 |
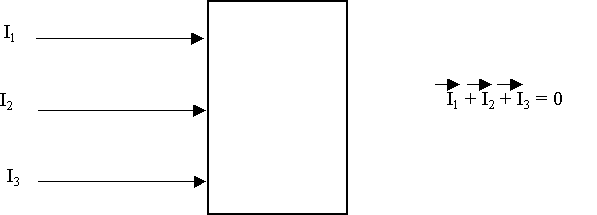
- On démontre que les intensités dans les fils de phase (ou en ligne) sont à n’importe quel moment, disposées deux dans le même sens, un en sens contraire.
- Si les trois intensités sont strictement égales en valeur et en phase, le montage sera dit équilibré.
|
|
- Les mêmes qu’en monophasé, à savoir S, P, Q. - Elles se calculent de manière différente, du fait de la présence de trois phases, au lieu d’une seule. Deux cas se présentent :
v
Le montage est déséquilibré. La
puissance active totale Pt = S
P consommées par chacune des phases. La puissance réactive totale Qt = S Q consommées par chacune des phases. La puissance apparente totale se calcule ainsi : S² = Pt² + Qt² Le facteur de puissance correspond à cos ( j ) = Pt / St
v
Le montage est équilibré. Dans ce cas on démontre que : S = U.I. P = U.I. 1,732. cos ( j ) = S . cos ( j ) Q
= U.I.
1,732 . sin
( j
) = S .sin ( j
) ( 1,732
= Racine carrée de trois ) Avec
U entre phases et I amenée par chaque fil de phase .
|