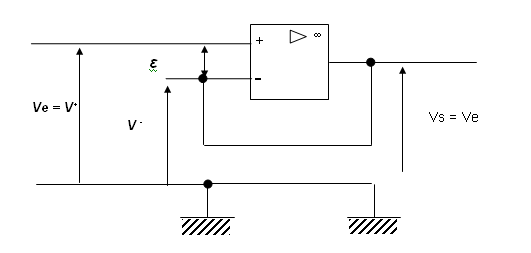
Remarque : L'appellation gain unité est une bêtise, car un gain s’exprime en dB. Et ici on veut signifier que le rapport Vs/ Ve = 1. Or, 20.log(1) = 0
Si l’on veut parler de gain, il serait juste de dire : amplificateur à gain nul. Sinon, le terme exact serait : amplificateur à coefficient d’amplification égale à l’unité.

Si l’on connaît la règle d’or.
V+ = V-
Il faut définir les deux termes et réaliser l’égalité.
(Se référer au cours sur les amplificateurs en régime linéaires.)
Le montage deviendrait :
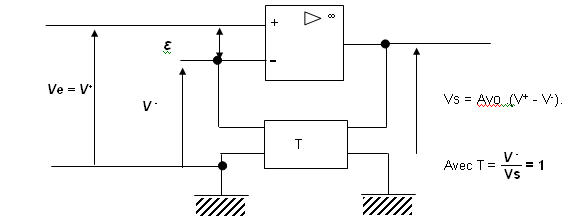
Selon les règles électrocinétiques appliquées à ce montage, nous obtiendrions, après bien des équations :
Pour obtenir T= 1, le plus simple est de mette directement un fil entre entrée V- et la sortie.
Ce type de montage est un des plus performants dans ce domaine. Si l’on revient à la courbe de réponse 20 log (Vs/ ε ) = f (ω) , avec ε = constante.
Il est possible de déterminer la bande passante en traçant une droite, pour un
gain = 20log (1) = 0 dB
Le montage transmettra de 0 Hz à f ≤ 100k Hz.
Les amplificateurs linéaires intégrés, sont appelés aussi : amplificateur opérationnel. Il s'agit d'un composant intégré bâti sur la structure de l'amplificateur différentiel. C'est-à-dire qu'il possède deux entrées. Chacune des deux entrées réalisent un effet opposé par rapport à l'autre.
Il possède une sortie unique référencée à la masse.
Ce composant le nécessite deux alimentations électriques référencées à une masse.
L'amplificateur linéaire intégré ne peut fonctionner seul. Grâce à des composants extérieurs rajoutés, il pourra amplifier et réaliser les opérations :
L'amplification se fera en tension.
Les opérations réalisées, seront de nature mathématique. Ce seront des sommes, où des différences, ou des produits, où des traitements logarithmiques. Il se peut que ce soit aussi un traitement sur les dérivés ou sur les primitives des tensions imposées sur les entrées.
Les opérations pourront être aussi de nature logique. Il sera possible de comparer les signaux.
Un amplificateur est en mode linéaire lorsque trois conditions sont réunies :
La sortie est reliée avec ou sans composants, vers une des deux entrées.
La différence des potentiels ε = (V -- V+), devra évoluer en sens inverse de la sortie. C'est-à-dire que si Vs augmente, ε devra diminuer et vice-versa.
La tension de sortie va être comprise entre +Vsat et – Vsat, sans atteindre ces deux valeurs extrêmes.
Lorsqu’un ALI est monté en linéaire, il y a obligatoirement une entrée qui est reliée à la sortie, via un quadripôle quelconque.
ε sera considéré comme ≈ 0, car Avo est énorme, sa valeur tendant vers l’infini, et la tension de sortie est comprise entre +Vsat et – Vsat , ce qui est relativement petit. Ce qui donne :
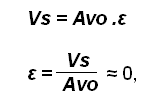
Nous considérerons l’Ali comme étant parfait !