
Le montage permet de :
D’additionner plusieurs différences de potentiels.
D’amplifier en tension, séparément, chacune des différences de potentiels.
Les grandeurs d’entrée pourront être de fréquences comprises entre 0 (continu), et une fréquence très élevée. La structure présentera une fréquence de coupure qui sera d’autant plus élevée que l’amplification sera faible.
La sortie sera en opposition de phase avec le résultat théorique de la somme des différences de potentiels des entrées
Il sera possible de choisir la valeur des impédances de chacune des entrées.
Réaliser une amplification en tension, d’une somme de plusieurs générateurs de tension.. Le coefficient d’amplification dépend exclusivement d’une paire de deux résistors satellites de "l'ALI".
La sortie sera en opposition de phase avec l'entrée, ce qui justifie l'appellation d'inverseur.

Pourquoi ? Parce V+ = 0 et V - = f (R1, R2, Vs) = V+ = 0
Nous allons vérifier si nous sommes en mode linéaire. Si c’est le cas, nous utiliserons la règle d’or (V+ = V-).
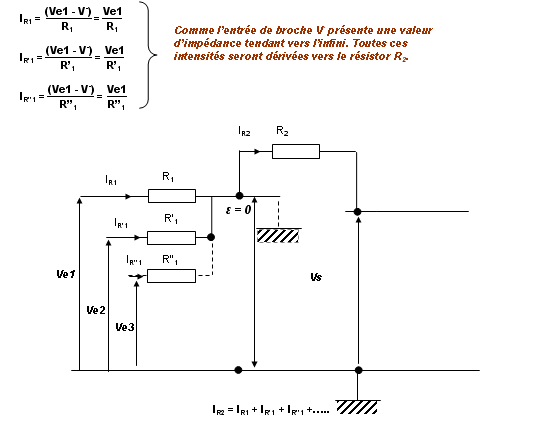
Nous déterminerons les différentes intensités qui circulent dans chacun des résistors « R1’ ‘’ ‘’’ », en fonction des différences de potentiels présentes aux entrées et de V - .
Nous déterminerons l’intensité qui traverse le résistor R2, en fonction de Vs et de V -.
Nous terminerons en appliquant la règle d’or V+ = V-
Les « ALIs» seront considérés parfaits.
Validation du mode.
La sortie de l’ALI est raccordée à une entrée.
Si Vs tend a augmenter V+ - V- aura tendance à diminuer.
-Vs sat < Vs <+ Vs sat
Le mode sera donc linéaire, donc V+ = V-
Il faut définir les deux termes et réaliser l’égalité.
V+ = 0---------------------------------------------------------simple constat.
V+ = V- = 0 ----------------------------------------------------C’est la règle d’or !
Remarque : la broche où se trouve V-, sera nommée et considérée, comme une masse virtuelle. C'est-à-dire un lieu, où le potentiel est nul !
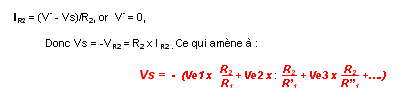
Il y a 3 grandeurs sinusoïdales à additionner. Les niveaux et fréquences des signaux d’entrée, sont respectivement de 2 V, 1Hz ; 1V, 3 Hz ; 0,5 V, 5 Hz.

Le schéma de montage :
Comme, R1 = R3 = R4
Alors :
R2/R1 =R2/R3 =R2/R4
La tension présente, en sortie de la structure :
La sortie, au point de mesures, présente bien la somme des tensions instantanées des entrées, fois le rapport R2/R1. La phase de la sortie est en opposition avec celles des entrées:
Ce type de montage va voir sa limite maximale en fréquence évoluer inversement avec le niveau d’amplification.
Si l’on revient à la courbe de réponse 20 log (Vs/ ε ) = f (ω) , avec ε = constante.
Il est possible de déterminer la bande passante en traçant une droite pour un gain :

Les amplificateurs linéaires intégrés, sont appelés aussi : amplificateur opérationnel. Il s'agit d'un composant intégré bâti sur la structure de l'amplificateur différentiel. C'est-à-dire qu'il possède deux entrées. Chacune des deux entrées réalise un effet opposé par rapport à l'autre.
Il possède une sortie unique référencée à la masse.
Ce composant le nécessite deux alimentations électriques référencées à une masse.
L'amplificateur linéaire intégré ne peut fonctionner seul. Grâce à des composants extérieurs rajoutés, il pourra amplifier et réaliser les opérations :
L'amplification se fera en tension.
Les opérations réalisées, seront de nature mathématique. Ce seront des sommes, où des différences, ou des produits, où des traitements logarithmiques. Il se peut que ce soit aussi un traitement sur les dérivés ou sur les primitives des tensions imposées sur les entrées.
Les opérations pourront être aussi de nature logique. Il sera possible de comparer les signaux.
Un amplificateur est en mode linéaire lorsque trois conditions sont réunies :
La sortie est reliée avec ou sans composants, vers une des deux entrées.
La différence des potentiels ε = (V -- V+). Devra évoluer en sens inverse de la sortie. C'est-à-dire que si Vs augmente, ε devra diminuer et vice-versa.
La tension de sortie va être comprise entre +Vsat et – Vsat, sans atteindre ces deux valeurs extrêmes.
Lorsqu’un ALI est monté en linéaire, il y a obligatoirement une entrée qui est reliée à la sortie, via un quadripôle quelconque :
ε sera considéré comme ≈ 0, car Avo est énorme, sa valeur tendant vers l’infini, et la tension de sortie est comprise entre +Vsat et – Vsat , ce qui est relativement petit. Ce qui donne :
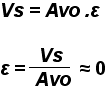
Ce qui amène V+ = V-
Nous considérerons l’Ali comme étant parfait !
Retour vers Technologie électronique de "Mistershoeélec"